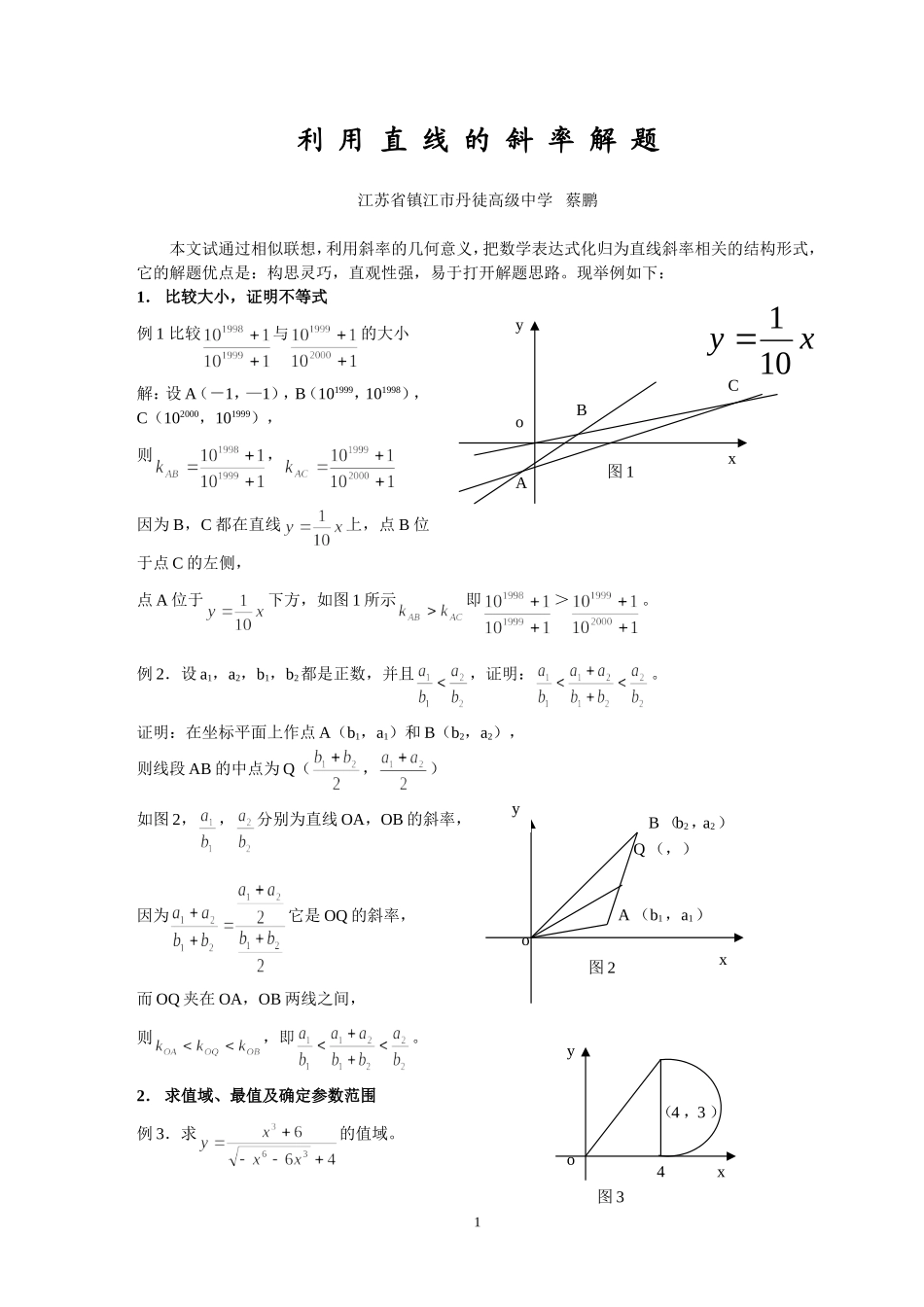
yxoABCxy101图1利用直线的斜率解题江苏省镇江市丹徒高级中学蔡鹏本文试通过相似联想,利用斜率的几何意义,把数学表达式化归为直线斜率相关的结构形式,它的解题优点是:构思灵巧,直观性强,易于打开解题思路。现举例如下:1.比较大小,证明不等式例1比较与的大小解:设A(-1,—1),B(101999,101998),C(102000,101999),则,因为B,C都在直线上,点B位于点C的左侧,点A位于下方,如图1所示即>。例2.设a1,a2,b1,b2都是正数,并且,证明:。证明:在坐标平面上作点A(b1,a1)和B(b2,a2),则线段AB的中点为Q(,)如图2,,分别为直线OA,OB的斜率,因为它是OQ的斜率,而OQ夹在OA,OB两线之间,则,即。2.求值域、最值及确定参数范围例3.求的值域。1A(b1,a1)Q(,)B(b2,a2)yox图2(4,3)yxo4图3解:令,,则。表示圆上的点与原点连线的斜率,,,故所求函数值域为。例4.当m为何值时,与的交点位于第二象限?解:直线方程变形为:,它表示过定点C(2,—1)斜率为m的直线系方程。又圆与y轴正半轴交于点A(0,),与x轴负半轴交于点B(—2,0),要求m的范围,只要求过点(2,—1)及((不含A、B)上任一点的直线的斜率的范围,即,∴。3.求等差、等比数列的有关问题(1)等差数列通项公式变形为,则点(n,)都在斜率为d的直线上(2)等差数列前项和公式:变形为:,则点()都在斜率为的直线上。(3)等比数列的通项公式,两边取对数得,即则点(n,)在斜率为lgq的直线上。例5在等差数列中{}中,,,则。解:由(1)可知,∴45。例6等差数列{}前m项和为30,前2m项和为100,求前4m项和.解:由(2)可知得,故=360。例7若一正项等比数列的第p,q,r项分别为x,y,z。2OxC(2,—1)ByA(0,)图4求证:(a>0,且a≠1)证明:点A(p,)(q,)(r,)共线,∴,即,经整理变形可得:。3