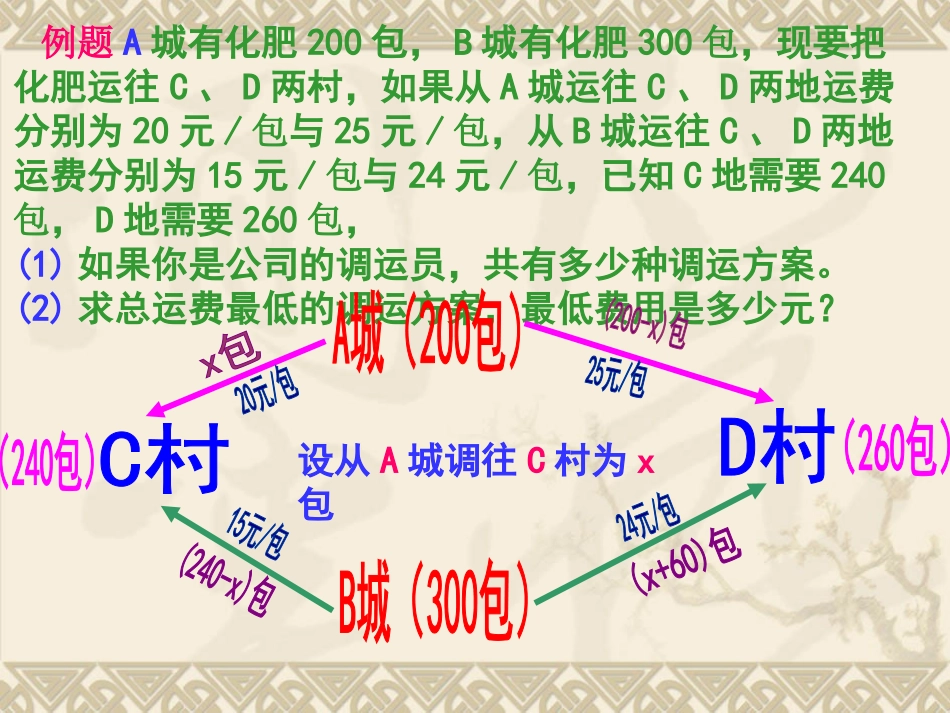
14.4课题学习---选择方案问题3例题A城有化肥200包,B城有化肥300包,现要把化肥运往C、D两村,如果从A城运往C、D两地运费分别为20元/包与25元/包,从B城运往C、D两地运费分别为15元/包与24元/包,已知C地需要240包,D地需要260包,(1)如果你是公司的调运员,共有多少种调运方案。(2)求总运费最低的调运方案,最低费用是多少元?设从A城调往C村为x包解;(1)设从A城调往C村x包化肥。所以运费最低调运方案是:CC村村DD村村AA城城00包包200200包包BB城城240240包包6060包包从A城调往C村0包;调往D村200包,从B城调往C村240包;调往D村60包。060024002000xxxx602402000xxxx2000x又 x为整数∴x=0,1,2‥‥200∴共有201种调运方案(2)y=20x+25(200-x)+15(240-x)+24(x+60)=4x+10040 y是x的一次函数且k=4>0∴y随x增大而增大∴当x最大时y最大又 0≤x≤200且x取整数∴x=0时,y有最小值y最小值=4×0+10040=10040(元)此时最低费用是10040元。1已知A市和B市各存机床12台和6台,现运往C市10台、D市8台.若从A市运一台到C市、D市各需4万元和8万元,若从B市运一台到C市、D市各需3万元和5万元.(1)设B市运往C市x台,求总费用y关于x的函数关系式.(2)若总费用不超过95万元,问共有几种调运方法?(3)求总费用最低的调运方法,最低费用是多少万元?解:(1)y=4(10-x)+8(x+2)+3x+5(6-x)=2x+8695862010060202xxxxx5.410620xxxxx解之得又 x为整数∴x=0,1,2,3,4∴共有5种调运方案5.40x所以运费最低调运方案是:CC市市DD市市AA市市1010台台22台台BB市市00台台66台台从A城调往C村10台;调往D村2台,从B城调往C村0台;调往D村6台。(3) 在y=2x+86中k=2>0∴y随x增大而增大又 0≤x≤4.5且x取整数∴x=0时,y有最小值y最小值=2×0+86=86(万万元元)此时最低费用是86万元。2从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨。从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米。设计一个调运方案使水的调运量(万吨·千米)尽可能小。解:设从A水库向甲地调水x万吨,总调运量为y万吨万吨··千米。千米。y=50x+45(x-1)+30(14-x)+60(15-x)=5x+1275010150140xxxx115140xxxx解之得141x又 在又 在y=5x+1275y=5x+1275中中k=5k=5>>00∴y随x增大而增大∴x=1时,y有最小值所以总调运量最低的方案是:甲库乙库A水库1万吨13万吨B水库14万吨0万吨3光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该收割机租赁公司商定的每天的租赁价格表如下每台甲型收割机的租金每台乙型收割机的租金A地区1800元1600元B地区1600元1200元(3)如果要使这50台收割机每天获得的租金最高,请你为光华农机公司提供一条合理化的建议(2)若使农机公司租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分配方案,并将各种方案设计出来;(1)设派往A地区x台乙型收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;解(1)y=1800(30-x)+1600(x-10)+1600x+1200(30-x)=54000-1800x+1600x-16000+1600x+36000-1200x=200x+74000 0300010030xxxx∴10≤x≤30且x取整数(2)令200x+74000≥79600200x≥5600x≥28又 10≤x≤30且x取整数∴28≤x≤30的整数∴x可取2828、、2929、、30.30.所以,有三种分配方案:(3) y是x的一次函数且k=200>0∴y随x的增大而增大∴当x最大=30时,y最大。因此,建议该公司:把30台乙型收割机全部派往A地区,把20台甲型收割机全部派往B地区。3001030xxxx甲型乙型AA地地BB地地AA地地BB地地方案方案1100台台2020台台3030台台00台台方案方案2211台台1919台台2929台台11台台方...