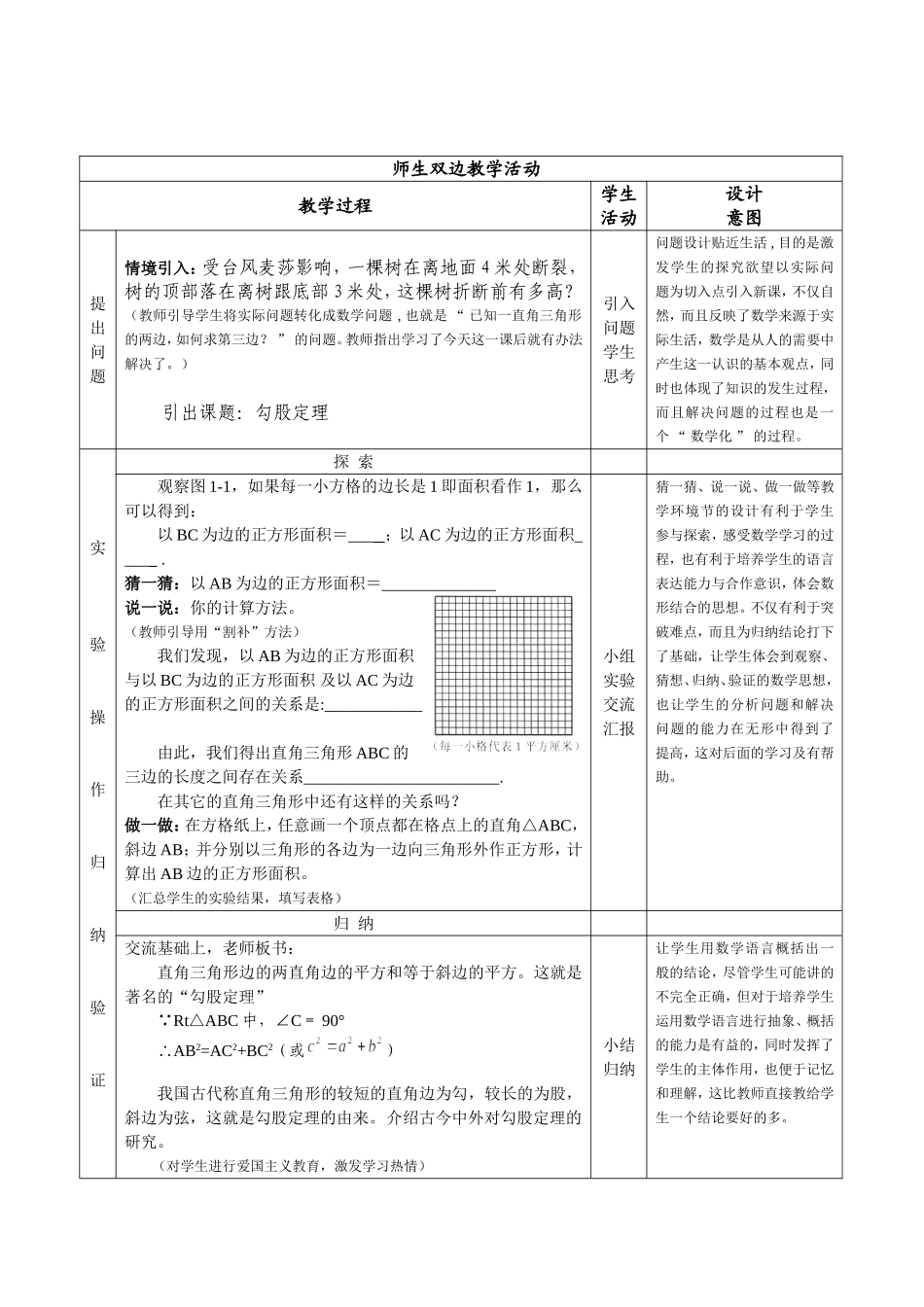
课题:“勾股定理”第一课时苏科版八年级上2.1节课前思考勾股定理是数学史上的一朵奇葩。它既是数学高度抽象的产物,又具有广泛的应用性。因此它的学习需要直观的感性经验作为心理支撑点,但数学的本质是理性的,没有理性的思考就不能构成真正意义上的数学学习。备课中,怎样实现感性的经验积累和理性的数学思考之间的有机结合,是我思考最多的地方。我根据数学知识具有过程和对象的双重特性,抓住数学知识的产生过程就是自然合理地提出问题和解决问题的过程。在教学设计中,以实际问题为切入口,对感性经验进行数学描述、数学观察、数学猜想、数学实验等直观思维操作后,做出数学概括,然后对所得到的结论进行验证及简单的应用(解决问题)。一、教材分析(一)教材所处的地位这节课是九年制义务教育课程标准实验教科书八年级上第二章第一节探索勾股定理第一课时,勾股定理是几何中几个重要定理之一,它揭示的是直角三角形中三边的数量关系,它可以解决直角三角形中的计算问题,是后续学习解直角三角形的主要根据之一,在实际生活中用途也很大。省教材在编写时将勾股定理的学习放在了实数这一章的开篇,沟通了勾股定理、平方根、立方根、实数之间的联系,体现了教材的整体性,突出了勾股定理的应用价值。勾股定理的探究教材以实际分析、拼图等活动为载体注意培养学生的动手操作能力和分析问题的能力,使学生获得较为直观的印象;再通过联系和归纳,得出勾股定理。学生通过对勾股定理的学习,可以在原有的基础上对直角三角形有进一步的认识和理解。(二)根据课程标准,本课的教学目标是:1、能说出勾股定理的内容,并能运用勾股定理进行简单的计算和实际运用。2、在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的数学过程,体会数形结合和特殊到一般的思想方法。3、通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。(二)本课的教学重点、难点及关键:重点:勾股定理的探索过程及其简单应用。难点:以直角三角形的斜边为边的正方形面积的计算。学生如何顺利探索勾股定理则是本节课的关键。二、教法与学法分析:教法分析:针对八年级学生的知识结构和心理特征,本节课可选择引导探索法,由浅入深由特殊到一般地提出问题。引导学生自主探究、动手实践、合作交流,这种教学理念反映了时代精神,有利于提高学生的思维能力,能有效地激发学生的思维积极性。采用多媒体教学,基本流程是:提出问题—实验操作—归纳验证—问题解决—课堂小结—布置作业六部分。学法分析:在教师的组织引导下,采用自主探究、动手实践、合作交流的研讨式学习方式,让学生思考问题,获取知识,掌握方法,借此培养学生动手、动脑、动口的能力,使学生真正成为学习的主体。三、教学过程设计见附表师生双边教学活动教学过程学生活动设计意图提出问题情境引入:受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?(教师引导学生将实际问题转化成数学问题,也就是“已知一直角三角形的两边,如何求第三边?”的问题。教师指出学习了今天这一课后就有办法解决了。)引出课题:勾股定理引入问题学生思考问题设计贴近生活,目的是激发学生的探究欲望以实际问题为切入点引入新课,不仅自然,而且反映了数学来源于实际生活,数学是从人的需要中产生这一认识的基本观点,同时也体现了知识的发生过程,而且解决问题的过程也是一个“数学化”的过程。实验操作归纳验证探索观察图1-1,如果每一小方格的边长是1即面积看作1,那么可以得到:以BC为边的正方形面积=___;以AC为边的正方形面积____.猜一猜:以AB为边的正方形面积=______________说一说:你的计算方法。(教师引导用“割补”方法)我们发现,以AB为边的正方形面积与以BC为边的正方形面积及以AC为边的正方形面积之间的关系是:____________由此,我们得出直角三角形ABC的三边的长度之间存在关系________________________.在其它的直角三角形中还有这样的关系吗?做一做:在方格纸上,任意画一个顶点都在格点上的直角△ABC,斜边AB;并分别以三角形的...