椭圆的定义与标准方程(成长课)课件(1)VIP免费

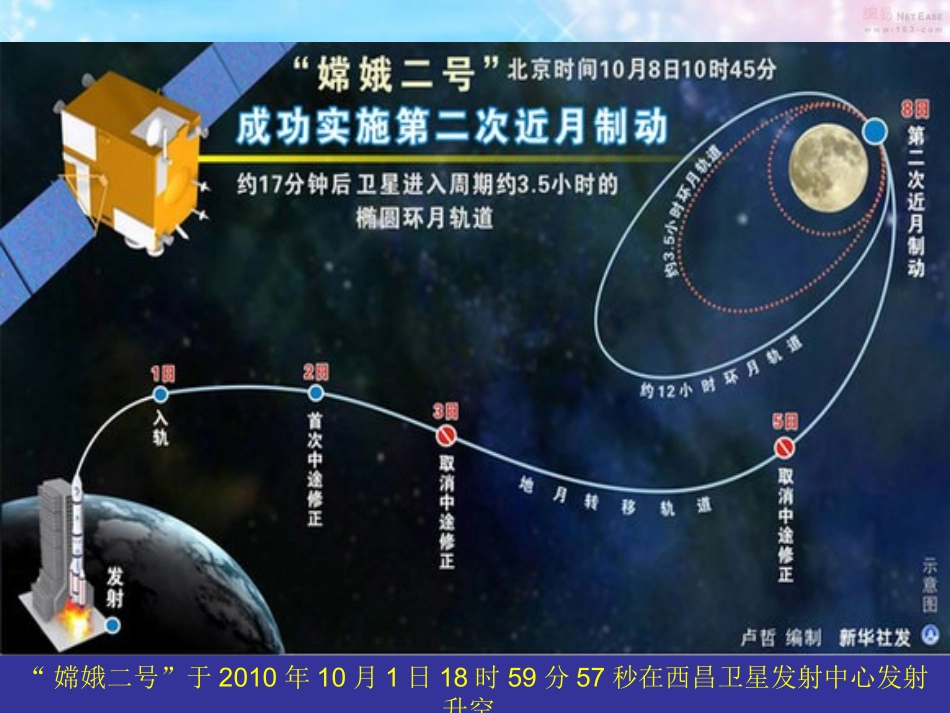
视频一视频二“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空金沙逸夫中学♦自然界处处存在着椭圆,我们如何用自己的双手画出椭圆呢?先回忆如何画圆分析：在这个运动过程中，什么是不变的？♦如何定义椭圆?椭圆的定义:平面上到两个定点F1,F2的距离之和为固定值(大于|F1F2|)的点的轨迹叫作椭圆。两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。问题：假设与两定点的距离之和为d,（2）当d=|F1F2|时，轨迹是什么？（3）当d<|F1F2|时，轨迹又是什么？（1）为什么要满足d>|F1F2|呢？d>|F1F2|时，是椭圆d=|F1F2|时，是线段d<|F1F2|时，不存在怎么推导椭圆的标准方程呢？♦求动点轨迹方程的一般步骤：1、建立适当的坐标系，用有序实数对（x,y）表示曲线上任意一点M的坐标;2、写出适合条件P（M）;3、用坐标表示条件P（M），列出方程;4、化方程为最简形式。坐标法坐标法♦探讨建立平面直角坐标系的方案OxyOxyOxyMF1F2方案一F1F2方案二OxyMOxy原则：尽可能使方程的形式简单、运算简单；(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)(对称、“简洁”)xF1F2Ｐ(x,y)0y设P(x,y)是椭圆上任意一点，椭圆的焦距|F1F2|=2c(c>0)，则F1、F2的坐标分别是(c,0)、(c,0).P与F1和F2的距离的和为固定值2a(2a>2c)（问题：下面怎样化简？）aPFPF2||||21222221)(||,)(||ycxPFycxPFaycxycx2)()(2222由椭圆的定义得，限制条件：由于得方程为什么假设为2a,而不直接用d表示?222222bayaxb22ba两边除以得).0(12222babyax设所以即,0,,2222cacaca),0(222bbca由椭圆定义可知整理得2222222)()(44)(ycxycxaaycx222)(ycxacxa2222222222422yacacxaxaxccxaa两边再平方，得)()(22222222caayaxca移项，再平方椭圆的标准方程刚才我们得到了焦点在x轴上的椭圆方程，如何推导焦点在y轴上的椭圆的标准方程呢？（问题：下面怎样化简？）aPFPF2||||21222221)(||,)(||cyxPFcyxPFacyxcyx2)()(2222由椭圆的定义得，限制条件：由于得方程aycxycxx2)()(2222轴焦点在).0(12222babyax)0(12222babxayy轴焦点在OXYF1F2M(-c,0)(c,0)YOXF1F2M(0,-c)(0,c))0(12222babyax)0(12222babxay♦椭圆的标准方程的特点：（1）椭圆标准方程的形式：左边是两个分式的平方和，右边是1（2）椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。（3）由椭圆的标准方程可以求出三个参数a、b、c的值。（4）椭圆的标准方程中，x2与y2的分母哪一个大，则焦点在哪一个轴上。2222+=1>>0xyabab2222+=1>>0xyabba分母哪个大，焦点就在哪个轴上222=+abc平面内到两个定点F1，F2的距离的和等于常数（大于F1F2）的点的轨迹12-,0,0，FcFc120,-0,，FcFc标准方程不同点相同点图形焦点坐标定义a、b、c的关系焦点位置的判断♦再认识！xyF1F2POxyF1F2PO22221.153xy，则a＝，b＝；则a＝，b＝；22222.146xy，则a＝，b＝；则a＝，b＝；55334466范例1，口答：则a＝，b＝；则a＝，b＝；则a＝，b＝．则a＝，b＝．337169.322yx6147.422yx2范例2.求下列椭圆的焦点坐标，以及椭圆上每一点到两焦点距离的和。1916)1(22yx12516)2(22yx143)3(22yx解：(1)椭圆方程具有形式12222byax其中3,4ba因此791622bac两焦点坐标为)0,7(),0,7(椭圆上每一点到两焦点的距离之和为82a(2)两焦点坐标为)0,3(),0,3(椭圆上每一点到两焦点的距离之和为102a(3)两焦点坐标为椭圆上每一点到两焦点的距离之和为3322a)0,63(),0,63(,10||||21PFPF分析：如图:即求满足下列条件的椭圆方程解：椭圆具有标准方程12222byax其中102,82ac因此91625222cab,5,4ac所求方程为192522yx范例3.若椭圆的两个焦点的坐标分别是，椭圆上一点P到两焦点距离和等于10.8||21FF)0,4(),0,4(21FF课堂训练,反思调节192522yx1椭圆上一点P到一个焦点的距离为5，则P到另一个焦点的距离为（）A....