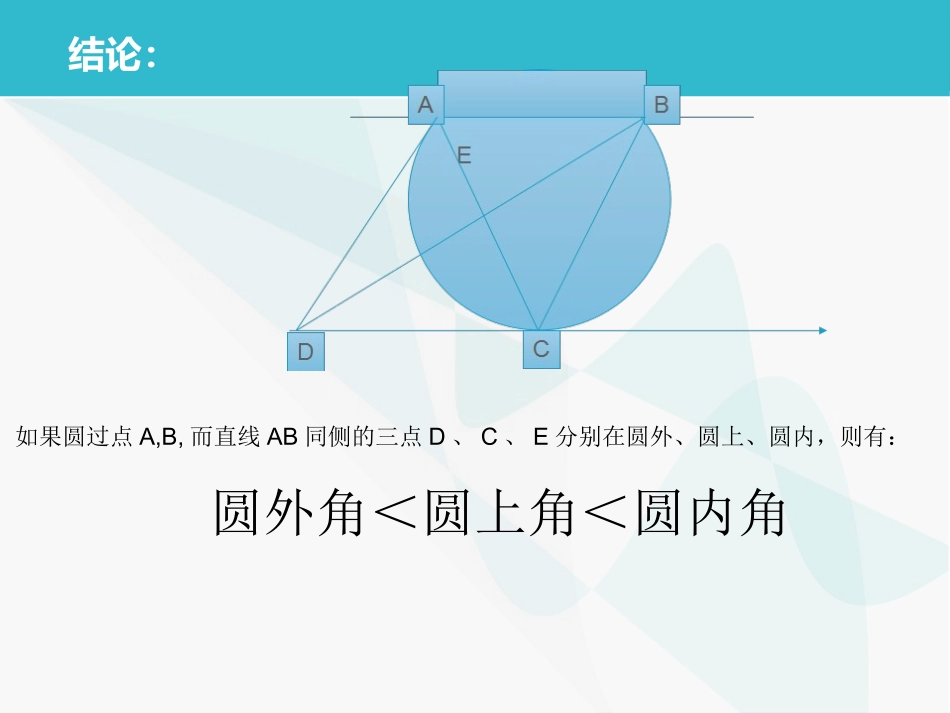
引入:课本:P32练习11题如图,点A在圆O内,点B在圆O外,点C,D在圆O上,试比较角CAD与角CBD的大小。结论:如果圆过点A,B,而直线AB同侧的三点D、C、E分别在圆外、圆上、圆内,则有:圆外角<圆上角<圆内角24.8综合与实践进球线路与最佳射门角射门点与射门角如图:ABC球门射门点射门角在不考虑其他因素的情况下:一般地,射门角越大,射门进球的可能性就越大运动员带球跑动的常见线路ABC球门射门点射门角ABC球门射门点射门角ABC球门射门点射门角一、横向跑动时的最佳射门点称:C点为直线m上的最佳射门点,∠ACB为直线m上的最佳射门角ABCDm问题1:ABCDm最佳射门角的大小与直线m到直线AB的距离有关,当直线m与AB的距离越近,最佳射门角就越大,射门进球的可能性也就越大。二、纵向跑动时的最佳射门点ABDCE注:当直线与过A、B的圆相切时,切点是最佳射门点?问题2ABDC已知AB=m,BD=n,当点C是直线l上的最佳射门点时,求CD的长问题3ABDC1、向左平移直线CD,观察最佳射门角有什么变化?2、当运动员跑动路线垂直穿过球门AB时,分析最佳射门点的位置此时,∠ACB越来越大,直线上没有最佳射门点三、斜向跑动时的最佳射门点你能探究运动员斜向跑动时,怎样找到最佳射门点吗?ABC球门射门点射门角