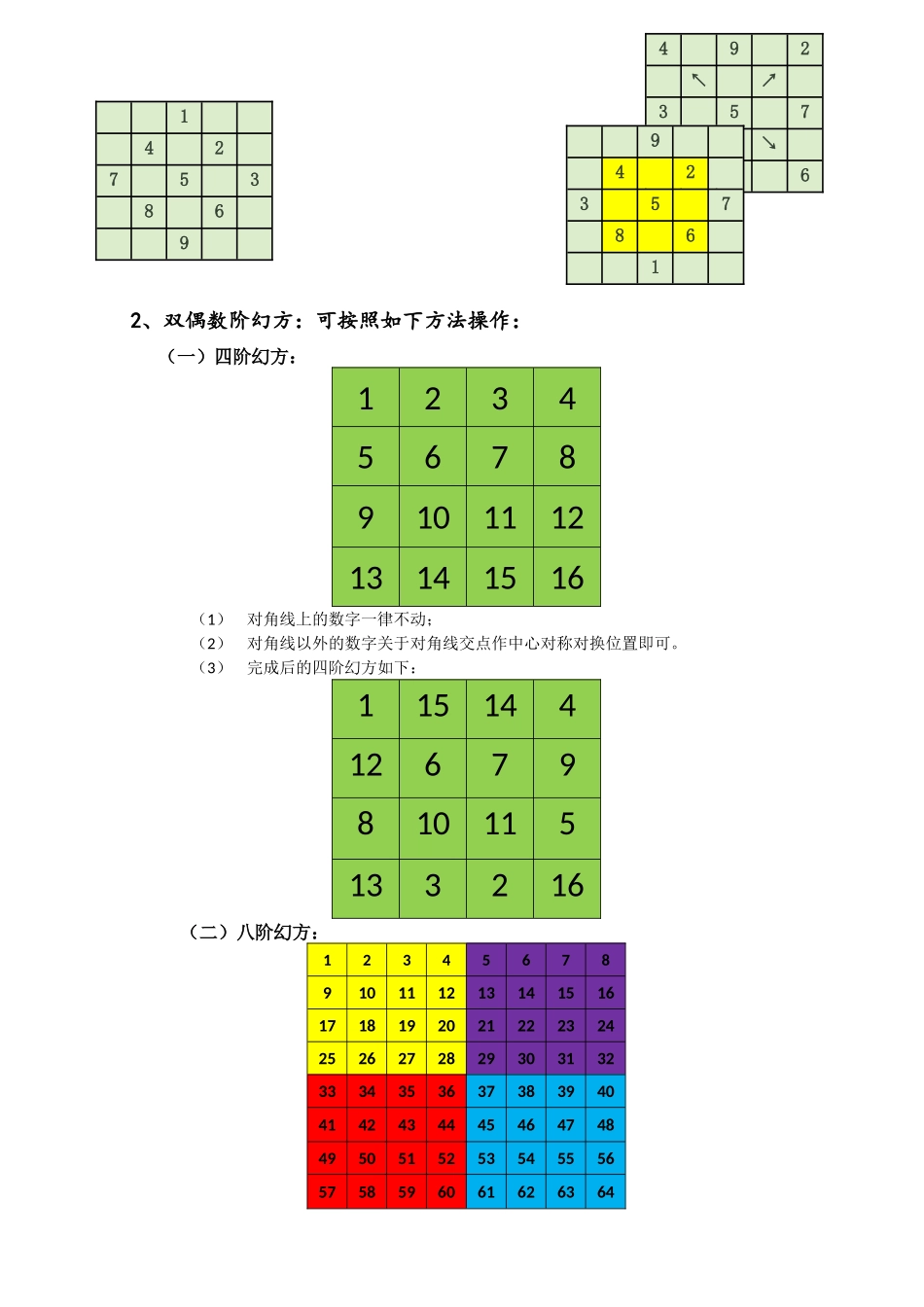
幻方的填写技巧一、N阶幻方的分类:1、奇数阶幻方:当n=2k+1时,称为奇数阶幻方。2、偶数阶幻方:(1)双偶数幻方:当n=4k=2×2k时,称为双偶数数阶幻方。(2)单偶数幻方:当n=4k+2=2׿时,称为单偶数阶幻方。二、幻方的填写方法:1、奇数阶幻方:可按照如下方法操作:(1)Merzirac法生成奇阶幻方在第一行居中的方格内放1,依次向右上方填入2、3、4…,如果右上方已有数字,则向下移一格继续填写。如下图用Merziral法生成的5阶幻方:17241815235714164613202210121921311182529Merzirac法,有人也叫楼梯法,我管它叫斜步法,即走X+Y斜步(数字按右上方顺序填入),-Y跳步(如果右上方已有数字或出了对角线,则向下移一格继续填写)。其实斜步法可以向4个方向依次填写数字,即右上、右下、左上、左下4个方向,每种斜步都可有2种跳步,即左(右)跳步、上(下)跳步。对于X+Y斜步相应的跳步可以为-X,-Y。【记住,跳步是X+Y斜步的X(或Y)相反方向即可。如右上方向斜步,跳步就为向左(或向下)一步;左下方向斜步,跳步就为向右(或向上)一步;等等等等】(2)杨辉“阳动阴静”法南宋杨辉不仅精通数学,而且精通易学,在他1275年所著的《续古摘奇算法》中,就对河图和洛书的数学问题进行了详尽的研究。其中对3阶幻方的排列,找出了一种奇妙的规律:“九子斜排,上下对易,左右相更,四维挺出,戴九履一,左三右七,二四为肩,六八为足”,清代,李光地的《周易折中》把杨辉所概括的这种排列排列原理为“阳动阴静”。2、双偶数阶幻方:可按照如下方法操作:(一)四阶幻方:12345678910111213141516(1)对角线上的数字一律不动;(2)对角线以外的数字关于对角线交点作中心对称对换位置即可。(3)完成后的四阶幻方如下:11514412679810115133216(二)八阶幻方:12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364142753869492↖↗357↙↘816942357861(1)对角线上的数字一律不动;(2)对角线以外的数字关于对角线交点作中心对称对换位置即可。(3)完成后的四阶幻方如下:163624559588561011535214154948181945442223412539382829353432333130363727264024424321204647171650511312545595776606132643、单偶数幻方的填法:n阶单偶幻方表示为4m+2阶幻方。将其等分为四分,成为如下图所示A、B、C、D四个2m+1阶奇数幻方。ACDBA用1至2m+1填写成(2m+1)2阶幻方;B用(2m+1)2+1至2*(2m+1)2填写成2m+1阶幻方;C用2*(2m+1)2+1至3*(2m+1)2填写成2m+1阶幻方;D用3*(2m+1)2+1至4*(2m+1)2填写成2m+1阶幻方;在A每行取m个小格(中心格及一侧对角线格为必换格,其余m-1格只要不是另一侧对角线格即可),也就是说在A中间一行取包括中心格在内的m个小格,其他行左侧边缘取m个小格,将其与D相应方格内交换;B与C任取m-1列相互交换。(一)六阶幻方:816261924357212325492222720352833171015303234121416313629131811(按奇数阶幻方填法按区域填写)六阶幻方之填法351626192433272123253192222720828331710153053412141643629131811(交换红色字体数字位置,其他数字位置不变)(二)十阶幻方:172418156774515865235714167355576466461320225456637072101219213606269715311182529616875525992997683904249263340988082899148303239417981889597293138454785879496783537444628869310077843643502734929918156774515840988071416735557644148188202254566370478587192136062697128869325296168755234172476839042492633652358289914830323966796139597293138457210129496783537444653111810077843643502759