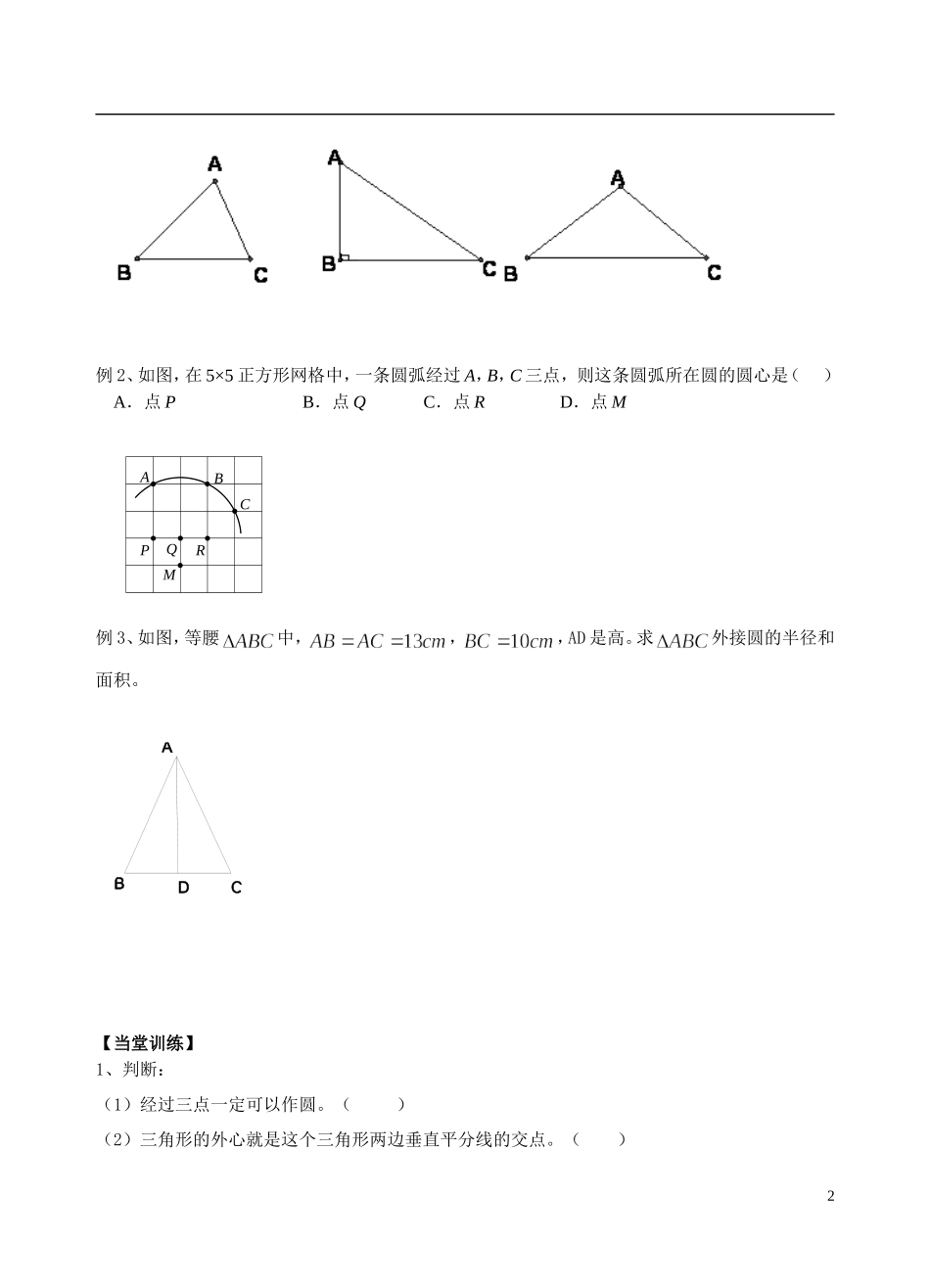
2.3确定圆的条件班级姓名【学习目标】1、经历不在同一条直线上的三点确定一个圆的探索过程。2、了解三角形的外接圆,三角形的外心,圆的内接三角形的概念,会过不在同一条直线上的三点作一个圆。。.【重点难点】重点:三角形的外接圆,外心,圆的内接三角形,会过不在同一条直线上的三点作一个圆。难点:不在同一条直线上的三点确定一个圆的探索过程【新知导学】读一读:阅读课本P50-P52想一想:如何确定一个圆?需要哪两个要素?练一练:1、操作(1):经过图中的点A作圆;(2):经过图中的A、B两点作圆;2、经过两点A、B可以作个圆,圆心在3、经过同一平面内三个点A、B、C能否作一个圆?如果能,请你作出这个圆,指出圆心的位置;如果不能,请你说明理由。【新知归纳】确定一个圆。叫做这个三角形的外接圆。叫做这个三角形的外心。叫做这个圆的内接三角形。【例题教学】例1、作出以下三角形的外接圆,并指出圆心的位置。(要求:尺规作圆,不写做法)1AABDCBAMRQABCP例2、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,则这条圆弧所在圆的圆心是()A.点PB.点QC.点RD.点M例3、如图,等腰中,,,AD是高。求外接圆的半径和面积。【当堂训练】1、判断:(1)经过三点一定可以作圆。()(2)三角形的外心就是这个三角形两边垂直平分线的交点。()2CBAOCBA(3)三角形的外心到三个顶点的距离相等。()(4)经过不在一直线上的四点能作一个圆。()2、三角形外接圆的圆心是()A.三个内角平分线的交点;B.三条边的中线的交点C.三条边垂直平分线的交点D.三边的三条高的交点3、如图:点A、B、C都在⊙O上,△ABC是⊙O的________三角形;⊙O是△ABC的________圆。4、经过已知点A,且半径为2cm的圆有个,这些圆的圆心的集合是:5、如图所示,O为△ABC的外心,若∠BAC=70°,则∠OBC=________.6、(1)解决“破镜重圆”的问题(作出破镜所在的圆):(2)设所画圆⊙O,已知AB=BC=60,∠ABC=120°,求此圆的半径。【课后巩固】1、判断正误1)任意一个三角形一定有一个外接圆.()2)任意一个圆一定有一内接三角形,并且只有一个内接三角形.()3)三角形的外心到三角形各个顶点的距离都相等.()2、下列命题不正确的是()A.三点确定一个圆B.三角形的外接圆有且只有一个3BAOyxC.经过一点有无数个圆D.圆的内接三角形有无数多个3、三角形的外心是三角形的______的圆心,它是_______的交点,它到_______的距离相等。4、如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,-2),则外接圆的圆心坐标是()A.(2,3)B.(3,2)C.(1,3)D.(3,1)5、如图,已知A、B两点的坐标分别为、(0,2),(1)作出过A、O、B三点的圆P,并求出点P的坐标。(2)Q是△AOB外接圆上的一点,且∠AOQ=45°,求点Q的坐标4