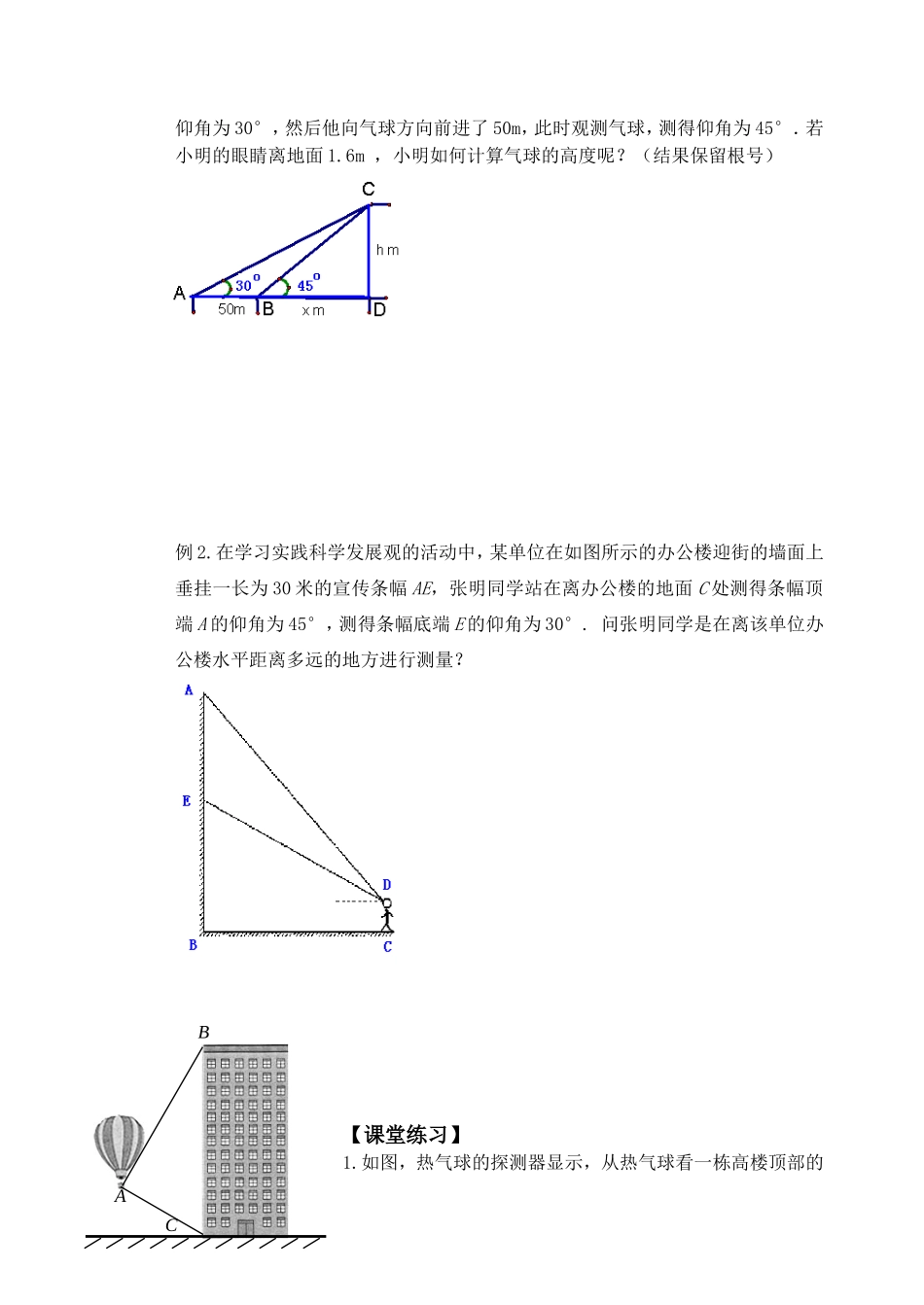
课题:7.6锐角三角函数的简单应用(2)班级姓名【学习目标】进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力。【课前自习】1.给出仰角、俯角的定义如右图,从下往上看,视线与水平线的夹角叫仰角,从上往下看,视线与水平线的夹角叫做俯角。右图中的∠1就是俯角,∠2就是仰角。2.如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为60,看这栋高楼底部的俯角为30,热气球与高楼的水平距离为66m,这栋高楼有多高?(本题只要求在图中标出仰、俯角。)【课堂助学】一、典型例题例1.为了测量停留在空中的气球的高度,小明先站在地面上某点观测气球,测得CAB仰角为30°,然后他向气球方向前进了50m,此时观测气球,测得仰角为45°.若小明的眼睛离地面1.6m,小明如何计算气球的高度呢?(结果保留根号)例2.在学习实践科学发展观的活动中,某单位在如图所示的办公楼迎街的墙面上垂挂一长为30米的宣传条幅AE,张明同学站在离办公楼的地面C处测得条幅顶端A的仰角为45°,测得条幅底端E的仰角为30°.问张明同学是在离该单位办公楼水平距离多远的地方进行测量?【课堂练习】1.如图,热气球的探测器显示,从热气球看一栋高楼顶部的CAB仰角为60,看这栋高楼底部的俯角为30,热气球与高楼的水平距离为66m,这栋高楼有多高?【课外作业】1.如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC为多少米?(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)2.九年级三班小亮同学学习了“测量物体高度”一节课后,他为了测得右图所放风筝的高度,进行了如下操作:ABCD6米52°35°(第1题图)(1)在放风筝的点处安置测倾器,测得风筝的仰角;(2)根据手中剩余线的长度出风筝线的长度为70米;(3)量出测倾器的高度米.根据测量数据,计算出风筝的高度约为多少米?3.如图,线段分别表示甲、乙两建筑物的高,,从点测得点的仰角为60°从点测得点的仰角为30°,已知甲建筑物高米.(1)求乙建筑物的高;(2)求甲、乙两建筑物之间的距离.ADBEC60°(第2题图)D乙CBA甲