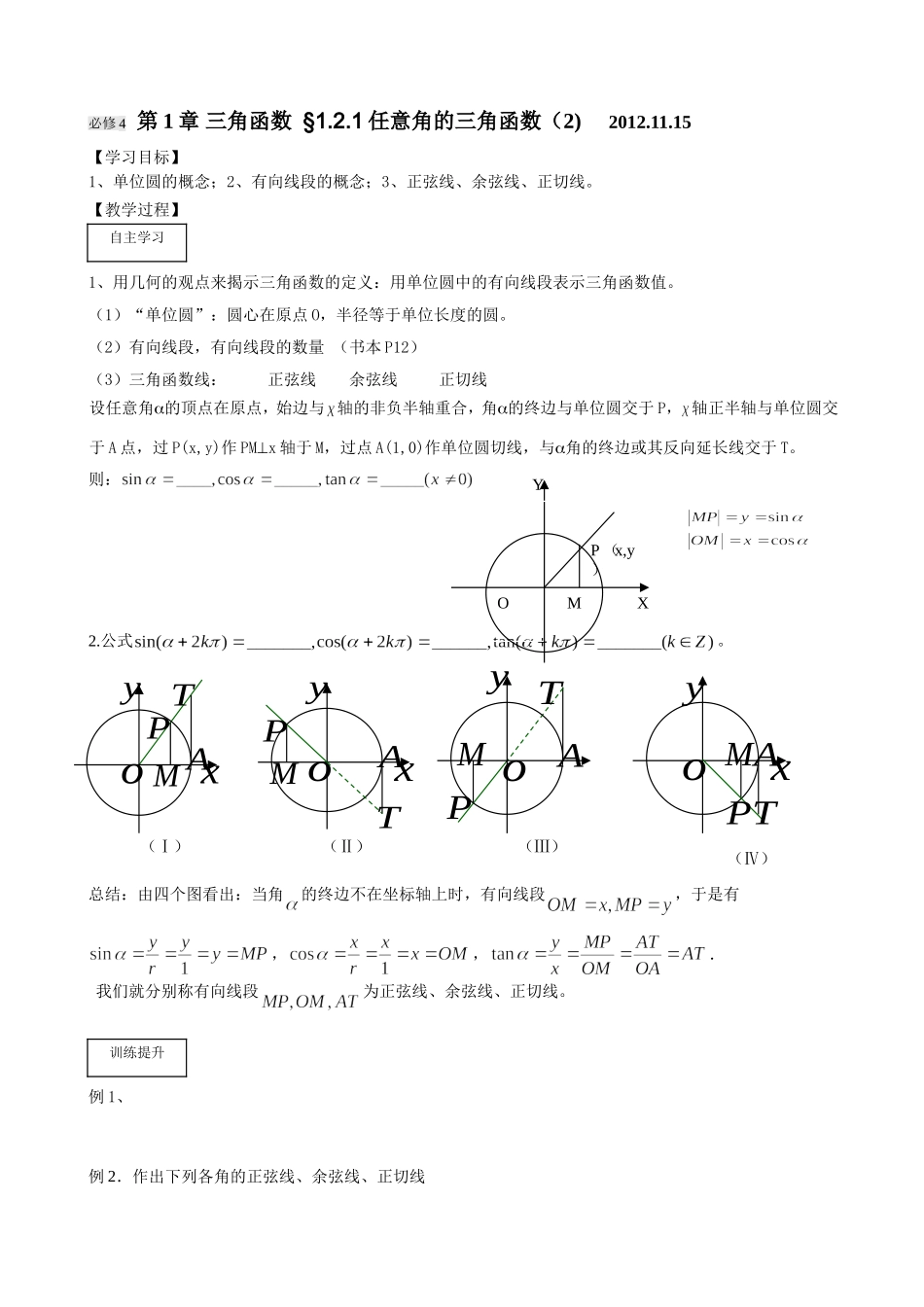
必修4第1章三角函数§1.2.1任意角的三角函数(2)2012.11.15【学习目标】1、单位圆的概念;2、有向线段的概念;3、正弦线、余弦线、正切线。【教学过程】1、用几何的观点来揭示三角函数的定义:用单位圆中的有向线段表示三角函数值。(1)“单位圆”:圆心在原点O,半径等于单位长度的圆。(2)有向线段,有向线段的数量(书本P12)(3)三角函数线:正弦线余弦线正切线设任意角的顶点在原点,始边与轴的非负半轴重合,角的终边与单位圆交于P,轴正半轴与单位圆交于A点,过P(x,y)作PMx轴于M,过点A(1,0)作单位圆切线,与角的终边或其反向延长线交于T。则:2.公式。总结:由四个图看出:当角的终边不在坐标轴上时,有向线段,于是有,,.我们就分别称有向线段为正弦线、余弦线、正切线。例1、例2.作出下列各角的正弦线、余弦线、正切线训练提升自主学习oxyMTPAoxyMTPAxyoMTPAyoMTPA(Ⅳ)(Ⅰ)(Ⅱ)(Ⅲ)MOP(x,y)XY(1)(2)(3)-(4)—例3、利用三角函数线比较下列各组数的大小:(1)与(2)tan与tan(3)cos与cos例4.在单位圆中,画出适合下列条件角a的终边的范围,并由此得出角a的范围(1)sin≥(2)cos<-(3)tan≥1变式训练:求下列函数的定义域:(1)y=1cos2x;(2)y=lg(3-4sin2x)例5、设是第二象限角,判断三角函数式的符号。1.小结:借助三角函数求角的值;判断三角函数在象限内的符号;三角函数的值域。【课后作业】1.当为第二象限角时,的值是__________________.评价小结2、已知,则满足条件的角的取值范围是_________________3、写出使的角的集合是_______________________4、设和分别是角的正弦线和余弦线,则给出以下不等式:①;②;③;④。其中正确的是___________。5.Sin1,cos1,tan1的由大到小关系是___________________6、从小到大的顺序是__________________。7.设,如果sin<0,cos2<0,那么的取值范围是________________________.8.若是第三象限角,则下列四个三角函数式中必为正数的是.(1)sin+cos(2)tan-sin(3)cotsec(4)sinsec9.确定下列三角函数值的符号:(填“正”“负”)(1)sin186(2)tan505(3)sin7.6(4)tan()(5)cos940(6)cos()10.求下列三角函数值:(1)(2)(3)(4)11.作出下列各角的正弦线、余弦线、正切线:(1)(2)(3)(4)12、利用单位圆写出符合下列条件的角的范围。(1)且1cos2x;(2);(3)且.13、求下列函数定义域(1)(2)(3)的定义域。14、已知,则为第几象限角?