5.1向量的概念及表示-pptVIP免费

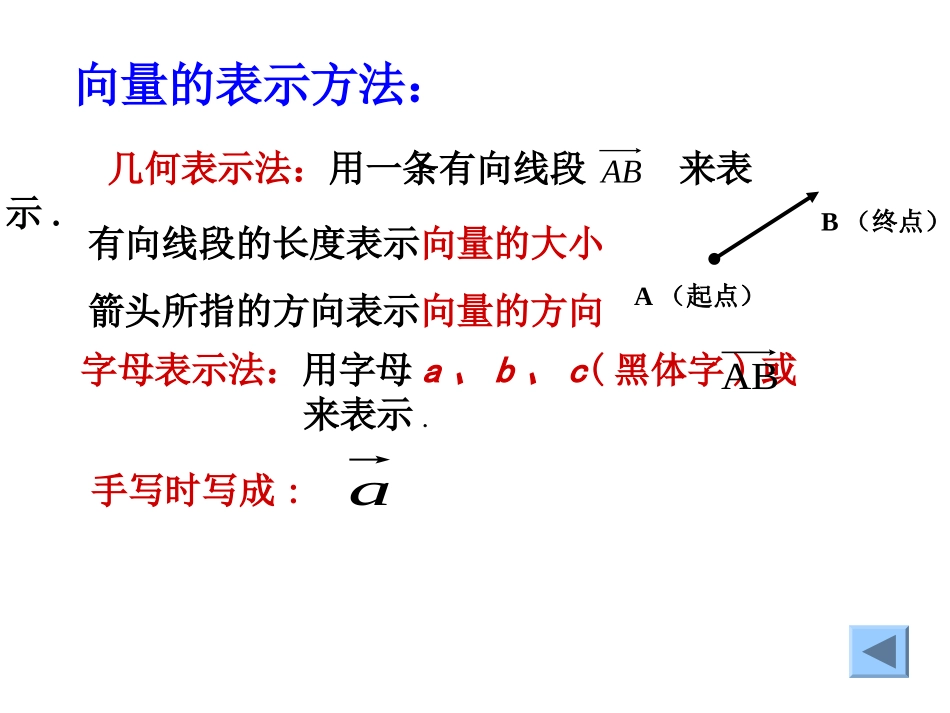
向量的概念及表示生活中有向量生活中用向量阅读课本P57－58完成下列问题:1.什么是向量?2.怎么表示向量表示向量?3.什么是向量的模?4.有哪些特殊向量?5.向量间有什么特殊关系?既有大小又有方向的量称为向量.1）几何表示；2）字母表示；指向量的长度AB�记作:||零向量单位向量平行向量共线向量相等向量相反向量字母表示法：用字母a、b、c(黑体字)或来表示.向量的表示方法：手写时写成:a有向线段的长度表示向量的大小箭头所指的方向表示向量的方向几何表示法：用一条有向线段来表示.ABA（起点）B（终点）AB2、单位向量：长度为1个单位长度的向量.零向量模为0，方向不确定.单位向量模为1，方向不一定相同.两个特殊向量：思考：平面直角坐标系内，起点在原点的单位向量，它们的终点的轨迹是什么图形？1、零向量：长度为0的向量.记作.0Oyx平行向量：规定零向量与任一向量平行.abab//记作：ef�ef��吗与是平行向量？方向相同或相反的非零向量叫做平行向量.任意一组平行向量都可以平移到同一直线上共线向量：平行向量又称共线向量abcabcabc称、、为线共向量.a//b//c相等向量：长度相等且方向相同的向量.相反向量:aa把与长度相等，方向相反的向量叫做的相反向量.-a记作：abab向量相等记作与，＝.a-(-)=？思考：AB�-=?巩固概念：(1)平行向量是否一定方向相反?(2)不相等向量是否一定不平行?(3)与零向量相等的向量是什么向量?(4)与任何向量都平行的向量是什么向量?(5)若两向量在同一直线上,则它们是什么?(6)非零向量相等的充要条件是什么?(7)共线向量一定在一条直线上吗?（不一定）（不一定）（零向量）（零向量）（共线向量）（方向相同，模相等）（不一定）四.例题1.如图,设O是正六边形ABCDEF的中心,分别写出图中与向量、、相等的向量.OAOAOAOAOBOCFEBAFEDCOMicrosoft¹«Ê½3.0OACBDO�OBDCEO�OCABFO�解：问题:(1)与相等吗?(2)与长度相等的向量有几个?(3)与共线的向量有哪几个?ED1、下列说法正确的是（）OABCAOBOCO�，、、；C.设是正的中心则向量是模相等的向量；A.共线的向量，若起点不同，则终点一定不同ABCDABCD�D.向量与是共线向量，则、、、四点必在一直线上.abab；B.若和都是单位向量，则=课堂练习C2、判断下列说法是否正确：abbcac（3）若=,=,则=;abbcac（4）若//,//,则//.abab=，则变∥题：；abab（2）若∥,则=;abab；=，则=变题：abab（1）若=;则=;相等向量与相反向量课堂小结：单位向量与零向量向量ABauuurr向量的表示：或向量的大小(长度、模)向量的方向有向线段平行向量(共线向量)