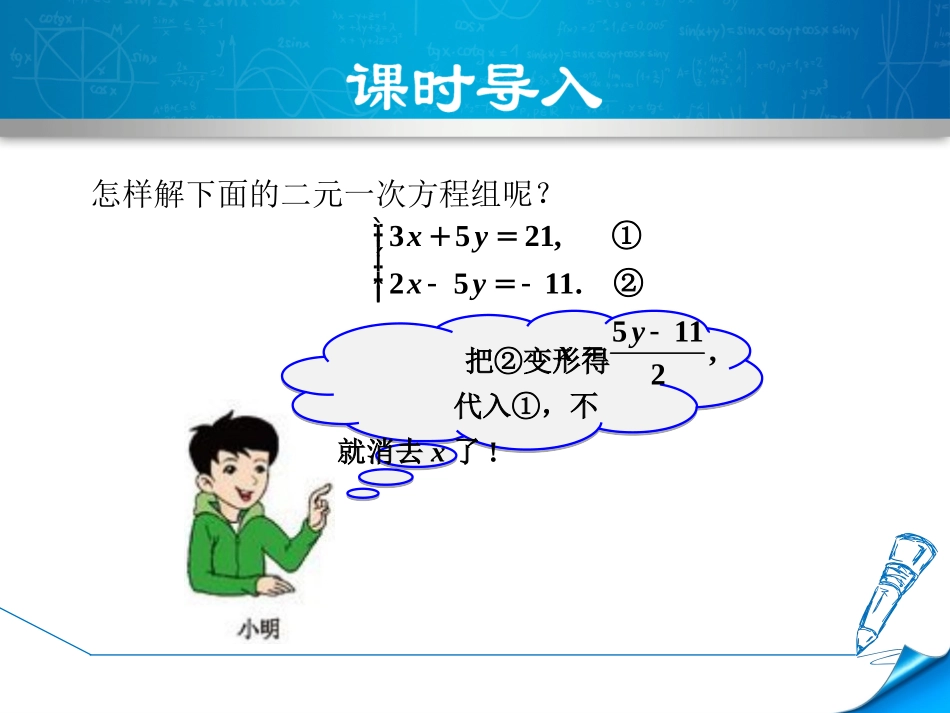
第八章二元一次方程组8.2消元——解二元一次方程组第2课时加减消元法把②变形得代入①,不就消去x了!怎样解下面的二元一次方程组呢?3521,2511.xyxyì+=ïïíï-=-ïî①②511,2yx-=按小丽的思路,你能消去一个未知数吗?把②变形得5y=2x+11,可以直接代入①呀!5y和-5y互为相反数……两个方程相加,可以得到5x=10,x=2.将x=2代入①,得6+5y=21,y=3.所以方程组23.xyì=ïïíï=ïî,3521,2511xyxyì+=ïïíï-=-ïî的解是11知识点直接加减消元思考:前面我们用代入法求出了方程组的解.这个方程组的两个方程中,y的系数有什么关系?利用这种关系你能发现新的消元方法吗?知1-导10,216.xyxyì+=ïïíï+=ïî①②(来自《教材》)知1-导(来自教材)这两个方程中未知数y的系数相等,②-①可消去未知数y,得x=6.把x=6代入①,得y=4.所以这个方程组的解是64.xyì=ïïíï=ïî,知1-导(来自教材)思考:联系上面的解法,想一想怎样解方程组3102.8,15108.xyxyì+=ïïíï-=ïî知1-导(来自教材)从上面两个方程组的解法可以看出:当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法(addition-subtractionmethod).用加减法解方程组:知1-讲371,3713.xyxyì-=-ïïíï+=ïî①②例1导引:两个方程中x的系数相同,y的系数互为相反数,这样可以把两个方程相加消去y,或者把两个方程相减消去x.方法一:①+②,得6x=12,解得x=2.把x=2代入②,得3×2+7y=13,解得y=1.所以原方程组的解为2,1.xyì=ïïíï=ïî解:知1-讲方法二:①-②,得-14y=-14,解得y=1.把y=1代入①,得3x-7×1=-1,解得x=2.所以原方程组的解为2,1.xyì=ïïíï=ïî22知识点先变形,再加减消元知2-导如果二元一次方程组的未知数的系数相同或互为相反数,我们可以运用加减法来解.那么对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗?用加减法解方程组:知2-讲3416,5633.xyxyì+=ïïíï-=ïî①②例2这两个方程中没有同一个未知数的系数相反或相等,直接加减这两个方程不能消元.我们对方程变形,使得这两个方程中某个未知数的系数相反或相等.分析:知2-讲(来自教材)解:①×3,得9x+12y=48.③②×2,得10x-12y=66.④③+④,得19x=114,即x=6.把x=6代入①,得3×6+4y=16,4y=-2,y=所以这个方程组的解是1.2-6,1.2xyìïïïíï-ïïî==例3解方程组:导引:方程组中,两个方程中y的系数的绝对值成倍数关系,方程②乘以3就可与方程①相加消去y.解:由②×3,得51x-9y=222,③由①+③,得59x=295,解得x=5.把x=5代入①,得8×5+9y=73,解得所以原方程组的解为知2-讲8973,17374.xyxyì+=ïïíï-=ïî①②5,11.3xyì=ïïïíï=ïïî11.3y=1用加减法解下列方程组:知2-练(来自《教材》)5+225,(1)3415;xyxyì=ïïíï+=ïî2+58,(2)325;xyxyì=ïïíï+=ïî2+36,(3)322.xyxyì=ïïíï-=-ïî3已知方程组由②×3-①×2可得到()A.-3y=2B.4y+1=0C.y=0D.7y=-8知2-练356,234,xyxyì-=ïïíï-=ïî①②知3-讲33知识点用加减法解方程组2台大收割机和5台小收割机同时工作2h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?例4(来自教材)知3-讲导引:如果1台大收割机和1台小收割机每小时各收割小麦xhm2和yhm2,那么2台大收割机和5台小收割机同时工作1h共收割小麦_____________hm2,3台大收割机和2台小收割机同时工作1h共收割小麦________hm2.由此考虑两种情况下的工作量.(来自教材)知3-讲解:设1台大收割机和1台小收割机每小时各收割小麦xhm2和yhm2.根据两种工作方式中的相等关系,得方程组去括号,得②-①,得11x=4.4.解这个方程,得x=0.4.2(25)3.6,5(32)8.xyxyì+=ïïíï+=ïî4103.6,15108.xyxyì+=ïïíï+=ïî①②(来自教材)知3-讲把x=0.4代入①,得y=0.2.因此,这个方程组的解是答:1台大收割机和1台小收...