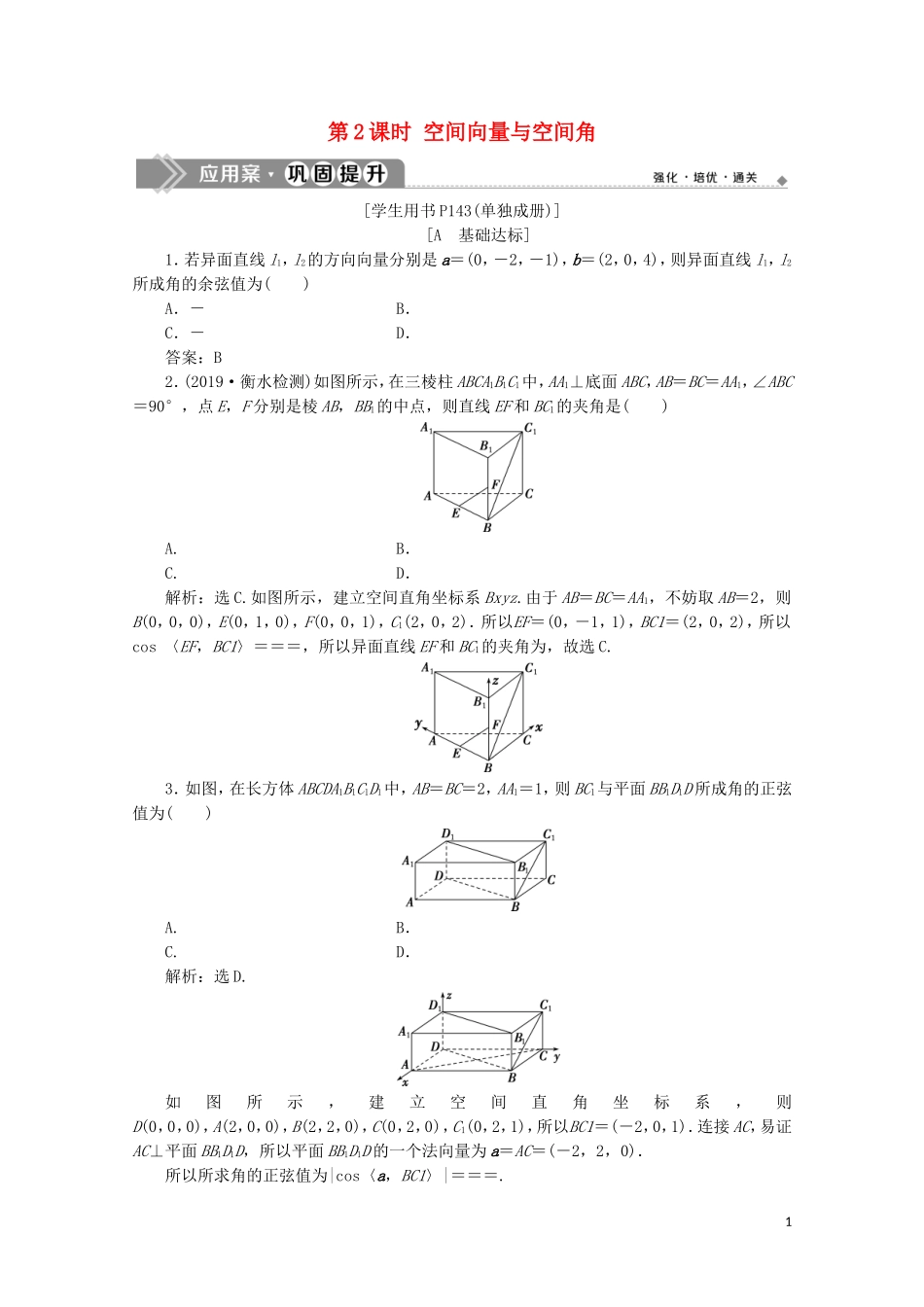
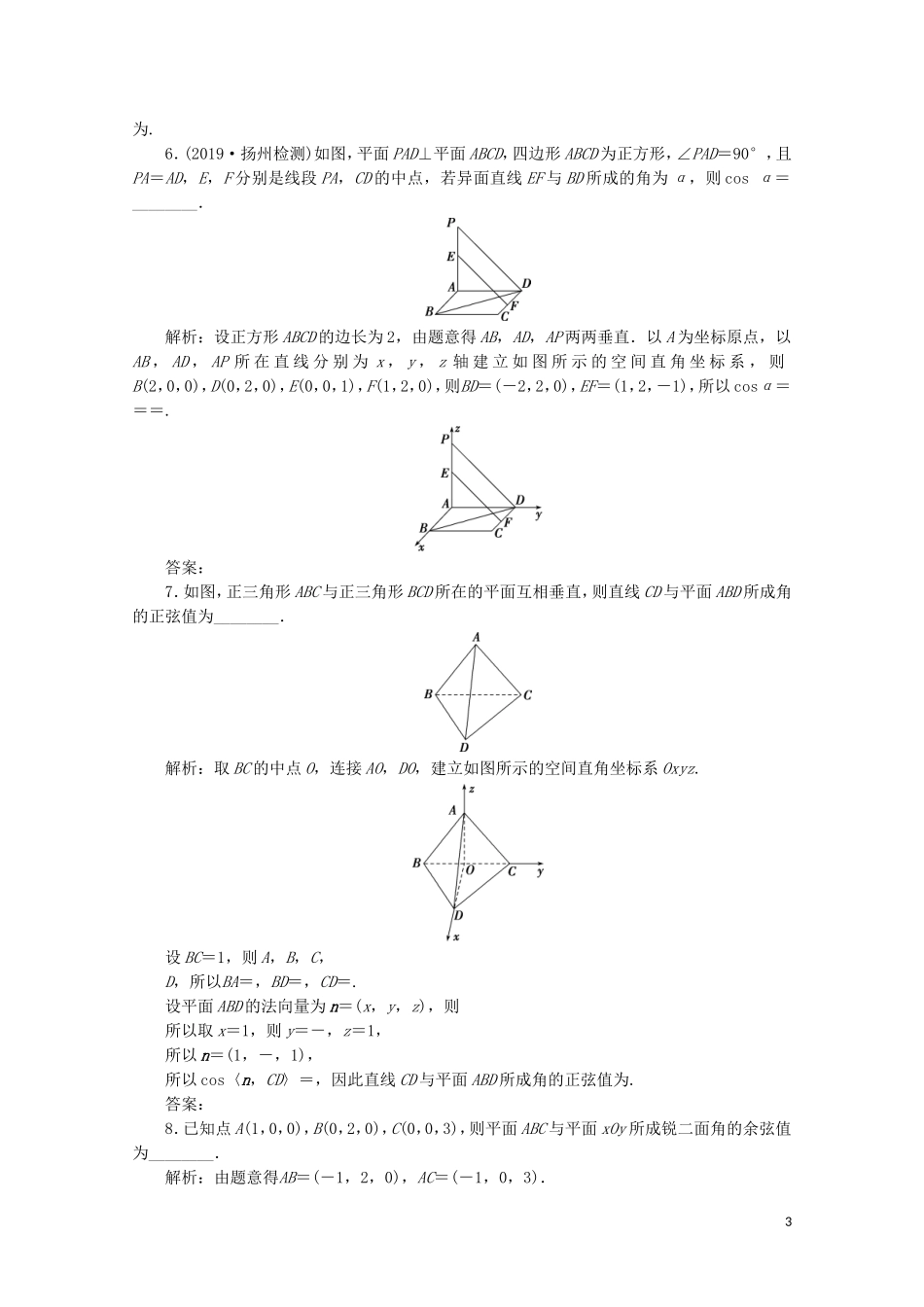
第2课时空间向量与空间角[学生用书P143(单独成册)][A基础达标]1.若异面直线l1,l2的方向向量分别是a=(0,-2,-1),b=(2,0,4),则异面直线l1,l2所成角的余弦值为()A.-B.C.-D.答案:B2.(2019·衡水检测)如图所示,在三棱柱ABCA1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1的夹角是()A.B.C.D.解析:选C.如图所示,建立空间直角坐标系Bxyz.由于AB=BC=AA1,不妨取AB=2,则B(0,0,0),E(0,1,0),F(0,0,1),C1(2,0,2).所以EF=(0,-1,1),BC1=(2,0,2),所以cos〈EF,BC1〉===,所以异面直线EF和BC1的夹角为,故选C.3.如图,在长方体ABCDA1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为()A.B.C.D.解析:选D.如图所示,建立空间直角坐标系,则D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),C1(0,2,1),所以BC1=(-2,0,1).连接AC,易证AC⊥平面BB1D1D,所以平面BB1D1D的一个法向量为a=AC=(-2,2,0).所以所求角的正弦值为|cos〈a,BC1〉|===.14.如图,过边长为1的正方形ABCD的顶点A作线段EA⊥平面AC,若EA=1,则平面ADE与平面BCE所成的二面角的大小是()A.120°B.45°C.150°D.60°解析:选B.以A为坐标原点,分别以AB,AD,AE所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则E(0,0,1),B(1,0,0),C(1,1,0),EB=(1,0,-1),EC=(1,1,-1).设平面BCE的法向量为n=(x,y,z),则有可取n=(1,0,1).又平面EAD的一个法向量为AB=(1,0,0),所以cos〈n,AB〉==,故平面ADE与平面BCE所成的二面角为45°.5.如图所示,已知四棱锥PABCD中,底面ABCD是菱形,且PA⊥平面ABCD,PA=AD=AC,点F为PC的中点,则二面角CBFD的正切值为()A.B.C.D.解析:选D.如图所示,设AC与BD交于点O,连接OF.因为底面ABCD为菱形,所以OB⊥OC,O为AC的中点,又F是PC的中点,所以OF∥AP,所以OF⊥平面ABCD,所以OB,OC,OF两两垂直.以O为坐标原点,OB,OC,OF所在直线分别为x,y,z轴建立空间直角坐标系Oxyz.设PA=AD=AC=1,则BD=,所以O(0,0,0),B(,0,0),F(0,0,),C(0,,0),OC=(0,,0),易知OC为平面BDF的一个法向量,由BC=(-,,0),FB=(,0,-),可得平面BCF的一个法向量为n=(1,,).所以cos〈n,OC〉=,sin〈n,OC〉=,所以tan〈n,OC〉=.故二面角CBFD的正切值2为.6.(2019·扬州检测)如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD,E,F分别是线段PA,CD的中点,若异面直线EF与BD所成的角为α,则cosα=________.解析:设正方形ABCD的边长为2,由题意得AB,AD,AP两两垂直.以A为坐标原点,以AB,AD,AP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,则B(2,0,0),D(0,2,0),E(0,0,1),F(1,2,0),则BD=(-2,2,0),EF=(1,2,-1),所以cosα===.答案:7.如图,正三角形ABC与正三角形BCD所在的平面互相垂直,则直线CD与平面ABD所成角的正弦值为________.解析:取BC的中点O,连接AO,DO,建立如图所示的空间直角坐标系Oxyz.设BC=1,则A,B,C,D,所以BA=,BD=,CD=.设平面ABD的法向量为n=(x,y,z),则所以取x=1,则y=-,z=1,所以n=(1,-,1),所以cos〈n,CD〉=,因此直线CD与平面ABD所成角的正弦值为.答案:8.已知点A(1,0,0),B(0,2,0),C(0,0,3),则平面ABC与平面xOy所成锐二面角的余弦值为________.解析:由题意得AB=(-1,2,0),AC=(-1,0,3).3设平面ABC的法向量为n=(x,y,z).由知令x=2,得y=1,z=,则平面ABC的一个法向量为n=(2,1,).平面xOy的一个法向量为OC=(0,0,3).由此易求出所求锐二面角的余弦值为=.答案:9.如图所示,直三棱柱ABCA1B1C1,∠BCA=90°,点F1是A1C1的中点,BC=CA=2,CC1=1.(1)求异面直线AF1与CB1所成角的余弦值;(2)求直线AF1与平面BCC1B1所成的角.解:(1)如图所示,分别以射线CA,CB,CC1为x,y,z轴的非负半轴建立空间直角坐标系,由BC=CA=2,CC1=1,得A(2,0,0),B(0,2,0),C1(0,0,1),...