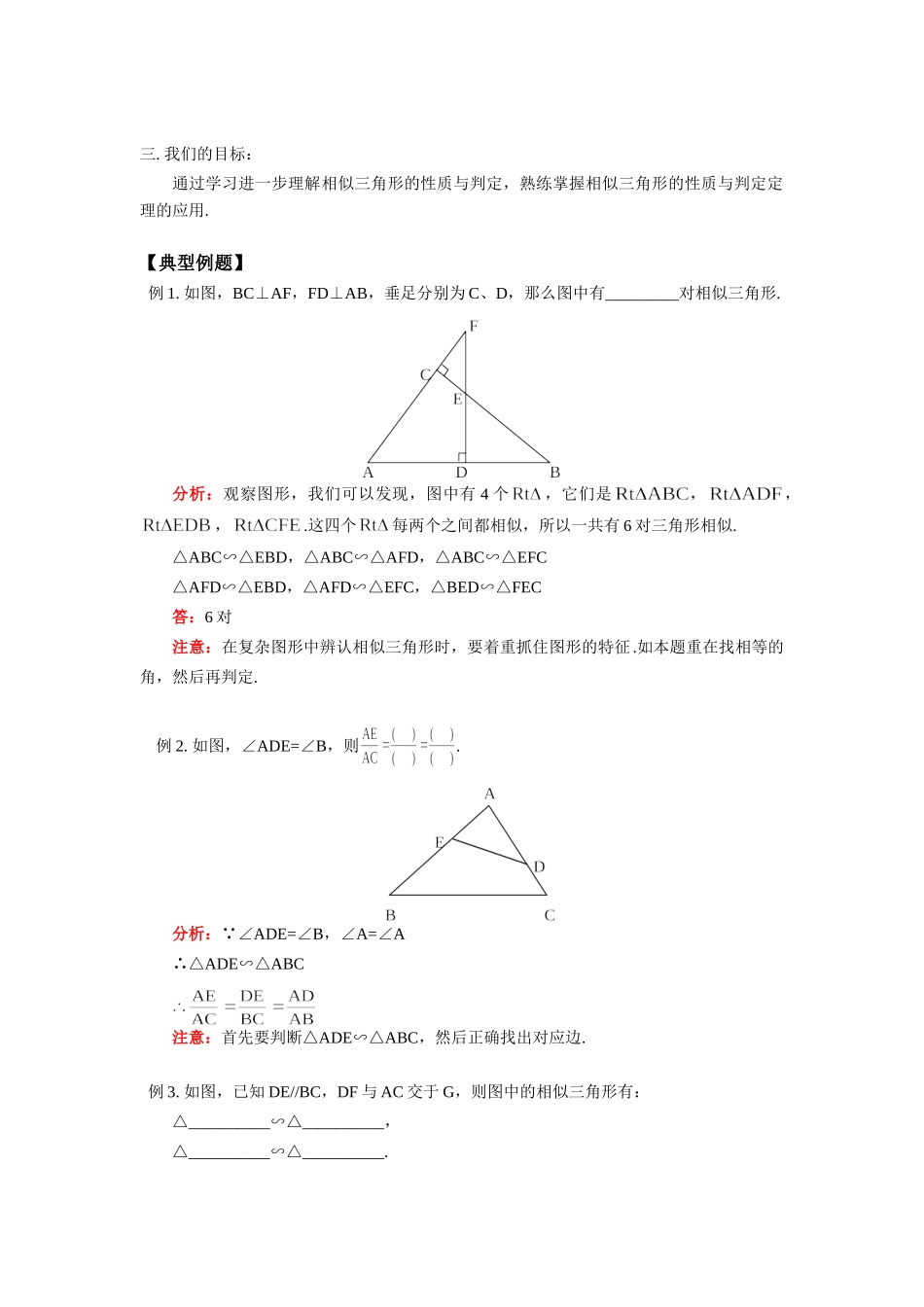
九年级数学相似三角形的性质与判定人教实验版【本讲教育信息】一.教学内容:相似三角形的性质与判定二.学习重点和难点1.相似三角形的性质:(1)相似三角形的对应角相等.(2)相似三角形的对应边的比相等.(3)相似三角形的对应线段成比例.(4)两个相似三角形的周长比等于相似比.(5)两个相似三角形的面积比等于相似比的平方.2.相似三角形的判定方法:(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.基本图形:推理格式:在△ABC中, DE//BC,∴△ADE∽△ABC.(2)如果两个三角形三组对应边的比相等,那么这两个三角形相似.基本图形:推理格式:在△ABC和△中,,∴△ABC∽△.(3)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.基本图形:推理格式:在△ABC和△中,,∠A=∠∽△.(4)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.基本图形:推理格式:在△ABC和△中, ∠A=∠,∠B=∠,∴△ABC∽△.三.我们的目标:通过学习进一步理解相似三角形的性质与判定,熟练掌握相似三角形的性质与判定定理的应用.【典型例题】例1.如图,BC⊥AF,FD⊥AB,垂足分别为C、D,那么图中有_________对相似三角形.分析:观察图形,我们可以发现,图中有4个,它们是,,.这四个每两个之间都相似,所以一共有6对三角形相似.△ABC∽△EBD,△ABC∽△AFD,△ABC∽△EFC△AFD∽△EBD,△AFD∽△EFC,△BED∽△FEC答:6对注意:在复杂图形中辨认相似三角形时,要着重抓住图形的特征.如本题重在找相等的角,然后再判定.例2.如图,∠ADE=∠B,则.分析: ∠ADE=∠B,∠A=∠A∴△ADE∽△ABC注意:首先要判断△ADE∽△ABC,然后正确找出对应边.例3.如图,已知DE//BC,DF与AC交于G,则图中的相似三角形有:△__________∽△__________,△__________∽△__________.答案:△ADE△ABC,△DEG△FCG.注意:要抓住DE//BC的条件,利用基本图形进行判定.例4.如图,AD=DF=FB,DE//FG//BC,则__________.答案:1:3:5分析: DE//FG//BC,∴△ADE∽△AFG∽△ABC又 AD=DF=FB∴AD:AF:AB=1:2:3.注意:要抓住AD=DF=FB,DE//FG//BC的条件,利用基本图形进行判定三角形相似,然后利用性质解题.例5.如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连结AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形,若有请写出来,并说明理由;若没有请说明理由.(3)求△BEC与△BEA的面积比.解:(1)DE=DA,EC=EA=EB.证明: ∠DEC=90°,∠BDC=60°,∴∠DCE=30°.,即DE=DA.∴∠DEA=∠DAE.又 ∠EDC=∠DEA+∠DAE=60°,∴∠DAE=∠DEA=30°.又 ∠BAC=45°,∴∠EAB=∠BAC-∠DAE=15°.又∠DEA=∠EAB+∠EBA,∴∠EBA=∠DEA-∠EAB=15°.∴∠EBA=∠EAB.∴EA=EB. ∠DCE=∠DAE=30°,∴EC=EA.∴EC=EA=EB.(2)①△ADE∽△CEA,或②△BCD∽△ACB①理由:△ADE,△CEA均为底角为30°的等腰△,∴△ADE∽△CEA.②理由: ∠CBD=∠CAB=45°,∠CDB=∠ABC=60°,∴△BCD∽△ACB.(3)过点A作AF⊥BD,交BD延长线于点F,则∠AFD=∠CED=90°.又∠ADF=∠CDE,∴△CED∽△AFD.,.即.【模拟试题】(答题时间:60分钟)一、选一选1.下列四条线段成比例的是()A.,3,2,B.3,2,6,4C.4,5,6,10D.12,8,11,162.用一个3倍放大镜照一个△ABC,下列说法正确的是()A.△ABC放大后,∠A是原来的3倍B.△ABC放大后,周长是原来的3倍C.△ABC放大后,面积是原来的3倍D.以上答案都不正确3.若,则等于()A.3:2B.2:3C.2:5D.5:24.下列两个三角形不一定相似的是()A.两个等边三角形B.两个全等三角形C.两个直角三角形D.有一个角是120°的两个等腰三角形5.如图所示,下列各式能使△ACB∽△DCA的是()A.B.C.D.6.过三角形一边上一点画直线与另一边相交,且截得的三角形与原三角形相似,那么最多可画这样的直线的条数是()A.1条B.2条C.3条D.4条7.如图所示,已知EF//BC,△AEF和梯形EBCF的面积分别为18,80。则AE:EB等于()A.:20B.3:7C.3:4D.9:498.如图所示,CD为Rt△ABC斜边上的高,AC:B...