高中数学 第二章 概率 6 正态分布同步测控 北师大版选修2-3-北师大版高二选修2-3数学试题VIP免费

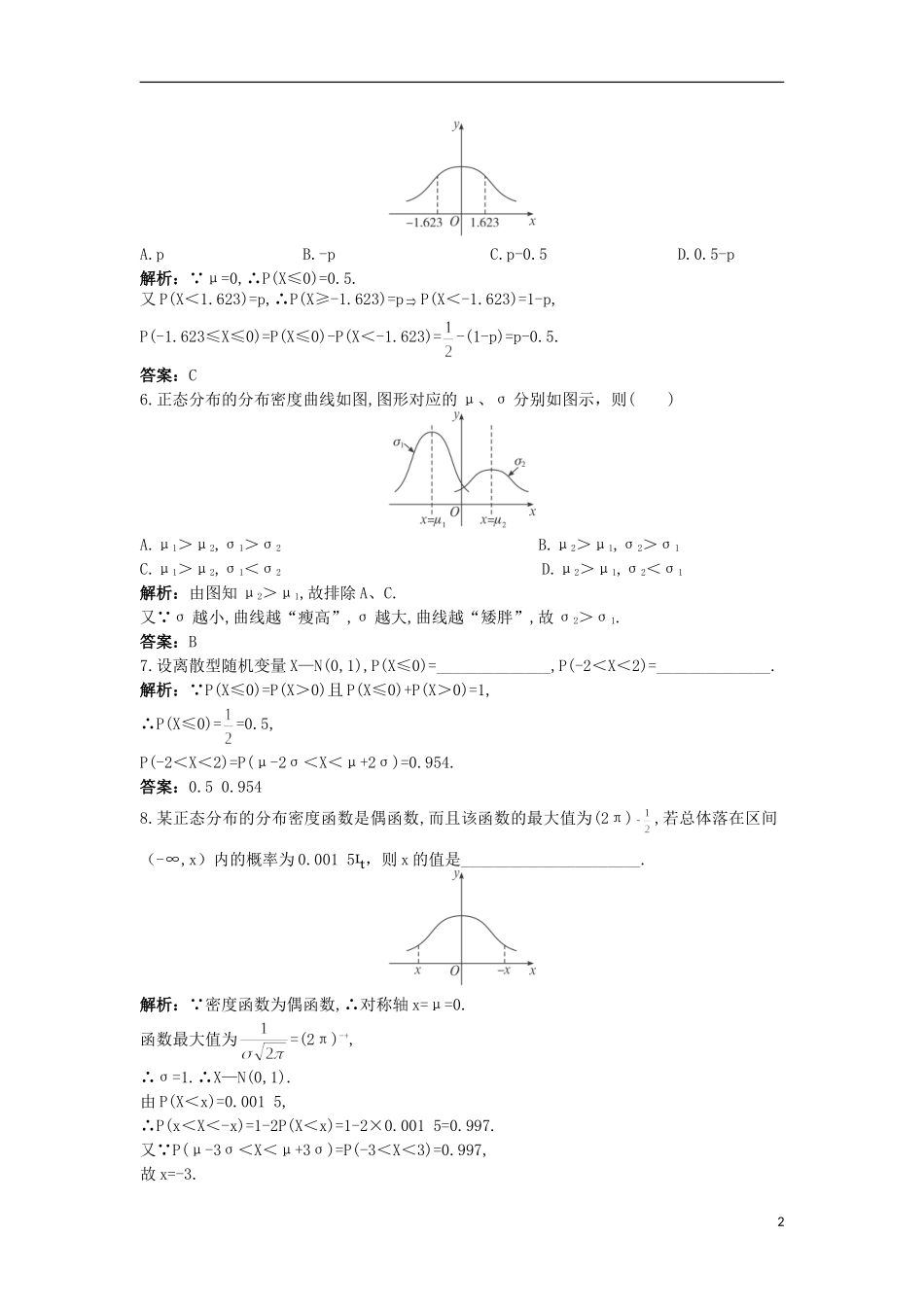
高中数学第二章概率6正态分布同步测控北师大版选修2-3我夯基，我达标1.下列图象可以作为正态分布密度曲线的是()答案：D2.对于正态分布N(0,1)的分布密度函数f(x)=,下列说法不正确的是()A.f(x)为偶函数B.f(x)的最大值是C.f(x)在x＞0时是单调减函数,在x≤0时是单调增函数D.f(x)是关于x=1对称的解析：f(x)的对称轴为x=μ=0,不是x=1.答案：D3.关于正态分布的分布密度曲线的途述:(1)曲线关于直线x=μ对称,并且曲线在x轴上方;(2)曲线关于y轴对称,且曲线的最高点的坐标是(0,);(3)曲线最高点的纵坐标是,且曲线无最低点;(4)当σ越大,曲线越“高瘦”,σ越小,曲线越“矮胖”.上述说法正确的是()A.(1)和(2)B.(2)和(3)C.(4)和(3)D.(1)和(3)解析：曲线的对称轴为x=μ,不一定是y轴,故(2)错;σ越大,曲线越“矮胖”,σ越小,曲线越“高瘦”,故(4)错.答案：D4.设随机变量X—N(μ,σ2),且P(X≤C)=P(X＞C)，则C()A.等于0B.等于μC.等于σD.与μ,σ无关解析：由曲线的对称性知x=μ是对称轴,故C=μ.答案：B5.设X—N(0,1),且P(X＜1.623)=p,那么P(-1.623≤X≤0)的值是()1A.pB.-pC.p-0.5D.0.5-p解析： μ=0,∴P(X≤0)=0.5.又P(X＜1.623)=p,∴P(X≥-1.623)=pP(X＜-1.623)=1-p,P(-1.623≤X≤0)=P(X≤0)-P(X＜-1.623)=-(1-p)=p-0.5.答案：C6.正态分布的分布密度曲线如图,图形对应的μ、σ分别如图示，则()A.μ1＞μ2,σ1＞σ2B.μ2＞μ1,σ2＞σ1C.μ1＞μ2,σ1＜σ2D.μ2＞μ1,σ2＜σ1解析：由图知μ2＞μ1,故排除A、C.又 σ越小,曲线越“瘦高”,σ越大,曲线越“矮胖”,故σ2＞σ1.答案：B7.设离散型随机变量X—N(0,1),P(X≤0)=______________,P(-2＜X＜2)=______________.解析： P(X≤0)=P(X＞0)且P(X≤0)+P(X＞0)=1,∴P(X≤0)==0.5,P(-2＜X＜2)=P(μ-2σ＜X＜μ+2σ)=0.954.答案：0.50.9548.某正态分布的分布密度函数是偶函数,而且该函数的最大值为(2π),若总体落在区间（-∞,x）内的概率为0.0015，则x的值是______________________.解析： 密度函数为偶函数,∴对称轴x=μ=0.函数最大值为=(2π)-+,∴σ=1.∴X—N(0,1).由P(X＜x)=0.0015,∴P(x＜X＜-x)=1-2P(X＜x)=1-2×0.0015=0.997.又 P(μ-3σ＜X＜μ+3σ)=P(-3＜X＜3)=0.997,故x=-3.2答案：-39.若X—N(3,1),求P(4＜X＜6).解： P(0＜X＜6)=P(μ-3σ＜X＜μ+3σ)=0.997,P(2＜X＜4)=P(μ-σ＜X＜μ+σ)=0.683.又 P(0＜X＜6)-P(2＜X＜4)=0.314,又由对称性知2·P(4＜X＜6)=0.314,∴P(4＜X＜6)=0.157.10.若随机变量X—N（μ,σ2）,则Y=也服从正态分布N(μ0,σ20),求μ0和σ0.解： X—N(μ,σ2),∴EX=μ,DX=σ2.而Y=也服从正态分布，只需求EY和DY,而EY=E()=EX-=,DY=D()=DX=σ2=σ, Y—N(μ0,σ20),故μ0=,σ0=.我综合，我发展11.设随机变量X—N(2,4),那么D(X)等于…()A.0.5B.1C.2D.4解析：由X—N(2,4),知σ2=4,即DX=4,D(X)=DX=×4=1.答案：B12.如果随机变量X—N(μ,σ2),且EX=3,DX=1,则P(0＜X≤1)等于()A.0.0215B.0.723C.0.215D.0.64解析：由EX=μ=3,DX=σ2=1,∴X—N(3,1),P(μ-3σ＜X＜μ+3σ)=P(0＜X＜6)=0.997,P(μ-2σ＜X＜μ+2σ)=P(1＜X＜5)=0.954,P(0＜X＜6)-P(1＜X＜5)=2P(0＜X≤1)=0.043,∴P(0＜X≤1)=0.0215.答案：A13.某地区高二女生的体重X(单位:kg)服从正态分布N(50,25)，若该地区共有高二女生2000人,则体重在50—65kg之间的女生人数为_______________________.解析：已知μ=50,σ=5,体重在50—65kg之间概率为P(50＜X＜65)=P(35＜X＜65)=P(μ-3σ＜X＜μ+3σ)==0.4985.∴体重在50—65kg之间的女生人数为2000×0.4985=997.3答案：99714.若函数f(x)=,则f(0),f(1),f(3)按由小到大排序应为____________________.解析：由f(x)知μ=1,2σ2=75,∴σ=6.f(x)的对称轴是x=1,图象如图所示.可知f(3)＜f(0)＜f(1).答案：f(3)＜f(0)＜f(1)15.某班学生共有48人,数学考试的分数服从正态分布,其平均分是80分,标准差为10分,则该班学生中成绩在70—90分之间的大约有__________________人.解析：先求该班学生的成绩在70—90分之间的概率.P(70＜X＜90)=P(μ-σ＜X＜μ+σ)=68.3%,∴该班学生的成绩在70—90分之间的人数为48×68.3%=32.784≈33(人).答案：3316....