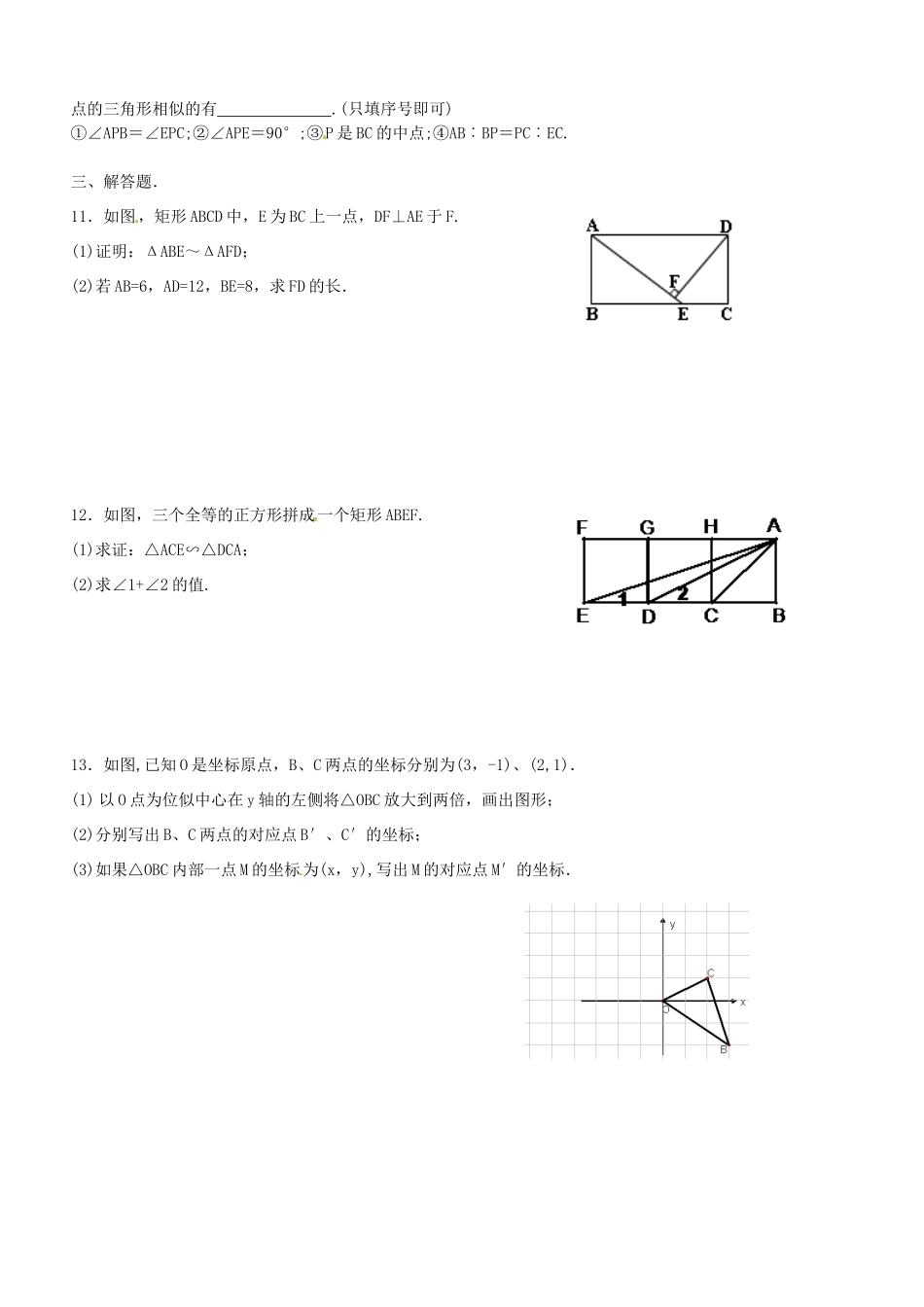
BDACPEABCDEF《相似形》测验班级姓名成绩一、选择题.1.如图,DE∥BC,EF∥AB,则图中相似三角形有()A.2对B.3对C.4对D.5对2.下列判断中,正确的是()A.各有一个角是30°的两个等腰三角形相似B.所有的菱形都相似C.所有的直角三角形都相似.D.所有的等边三角形都相似3.已知=,那么=()A.B.C.D.4.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为()A.B.C.D.5.如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则CD的长为()A.1B.C.2D.6.如图,ABCD和A’B’C’D’的面积之比为()A.1︰2B.1︰4C.4︰1D.1︰二、选择题.7.甲、乙两地的实际距离20千米,则在比例尺为1∶1000000的地图上两地间的距离应为厘米.8.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,则较小三角形的周长为________cm.9.如右图所示为农村一古老的捣碎器,已知支撑柱的高为0.3米,踏板长为1.6米,支撑点到踏脚的距离为0.6米,现在踏脚着地,则捣头点上升了米.10.如图,ABCD是正方形,E是CD边上的动点,P是BC边上的动点,在下列条件中,若只添加一个条件,就能使得△ABP与以E、C、P为顶ADEB点的三角形相似的有.(只填序号即可)①∠APB=∠EPC;②∠APE=90°;③P是BC的中点;④AB︰BP=PC︰EC.三、解答题.11.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)证明:ΔABE~ΔAFD;(2)若AB=6,AD=12,BE=8,求FD的长.12.如图,三个全等的正方形拼成一个矩形ABEF.(1)求证:△ACE∽△DCA;(2)求∠1+∠2的值.13.如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍,画出图形;(2)分别写出B、C两点的对应点B′、C′的坐标;(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.14.△ABC中,BC=10,DG=5,D、G分别在边AB、AC上,DEFG是一个矩形,DE=4,线段AH垂直BC交DG于M,求AM.15.已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?16.如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,若△AED与以M、N、C为顶点的三角形相似,求CM的值.MABCHDEGFEBDACNM17.如图,三角形纸片ABC,,AB=4,BC=2.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,在BC边上是否存在一点D,使以D,E,F为顶点的三角形和以D,E,B为顶点的三角形相似?若存在.求出相似比;若不存在,说明理由.