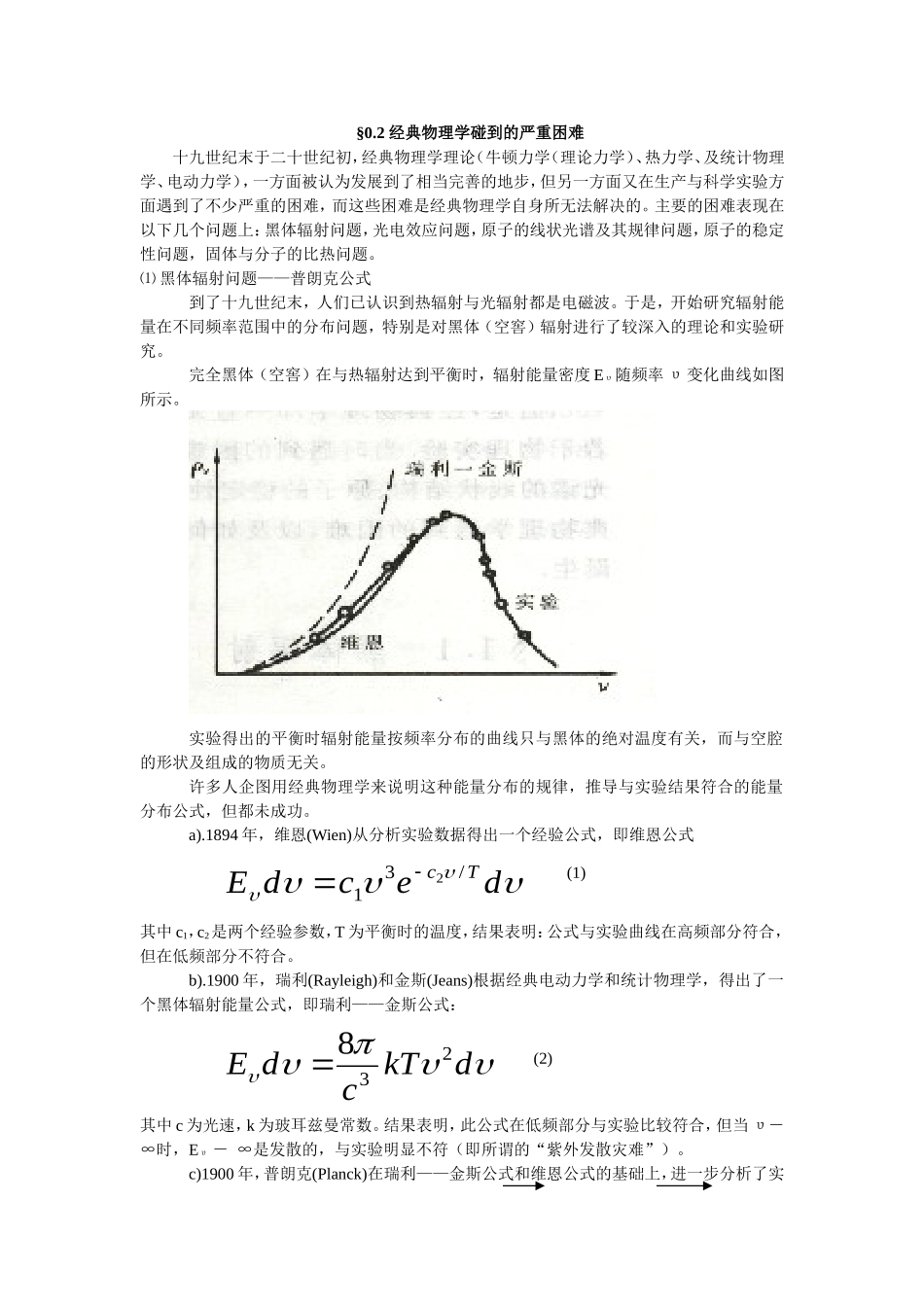
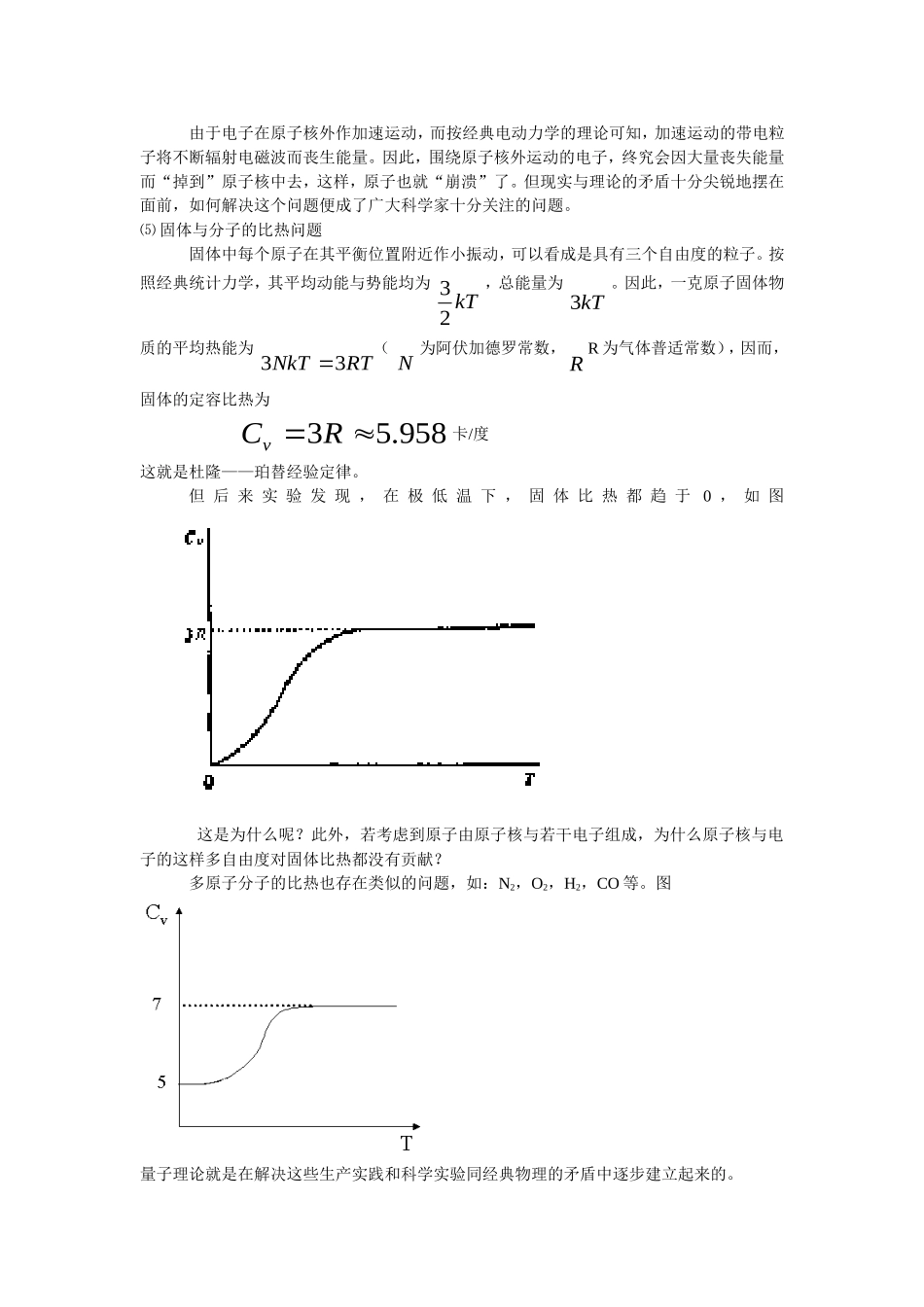
§0.2经典物理学碰到的严重困难十九世纪末于二十世纪初,经典物理学理论(牛顿力学(理论力学)、热力学、及统计物理学、电动力学),一方面被认为发展到了相当完善的地步,但另一方面又在生产与科学实验方面遇到了不少严重的困难,而这些困难是经典物理学自身所无法解决的。主要的困难表现在以下几个问题上:黑体辐射问题,光电效应问题,原子的线状光谱及其规律问题,原子的稳定性问题,固体与分子的比热问题。⑴黑体辐射问题——普朗克公式到了十九世纪末,人们已认识到热辐射与光辐射都是电磁波。于是,开始研究辐射能量在不同频率范围中的分布问题,特别是对黑体(空窖)辐射进行了较深入的理论和实验研究。完全黑体(空窖)在与热辐射达到平衡时,辐射能量密度Eυ随频率υ变化曲线如图所示。实验得出的平衡时辐射能量按频率分布的曲线只与黑体的绝对温度有关,而与空腔的形状及组成的物质无关。许多人企图用经典物理学来说明这种能量分布的规律,推导与实验结果符合的能量分布公式,但都未成功。a).1894年,维恩(Wien)从分析实验数据得出一个经验公式,即维恩公式decdETc/312(1)其中c1,c2是两个经验参数,T为平衡时的温度,结果表明:公式与实验曲线在高频部分符合,但在低频部分不符合。b).1900年,瑞利(Rayleigh)和金斯(Jeans)根据经典电动力学和统计物理学,得出了一个黑体辐射能量公式,即瑞利——金斯公式:dkTcdE238(2)其中c为光速,k为玻耳兹曼常数。结果表明,此公式在低频部分与实验比较符合,但当υ-∞时,Eυ-∞是发散的,与实验明显不符(即所谓的“紫外发散灾难”)。c)1900年,普朗克(Planck)在瑞利——金斯公式和维恩公式的基础上,进一步分析了实验曲线,得到了一个很好的经验公式,即有名的普朗克公式:(3)不难看出:当υ-∞时,公式(3)-公式(1)当υ-0时,公式(3)-公式(2)普朗克提出这个公式后,许多实验物理学家用它来分析当时最精确的实验数据,发现符合的很好。于是,人们开始认识到,这绝非偶然的巧合,在这公式中一定蕴藏着一个非常重要,但是尚未被人们揭示出的科学原理。这就是有名的黑体辐射问题。⑵光电效应问题1888年,赫兹(Hertz)发现了光电效应,但对其机制还不清楚。直到1896年,汤姆逊(Thomson)通过气体放电现象及阴极射线的研究发现了电子,才认识到:“这是由于紫外线照射,大量电子从金属表面逸出的现象。”经过实验研究,发现光电效应呈现下列几个特点:a).对于一定的金属材料做成的电极,有一个确定的临界频率υ0,当照射光频率υ<υ0时,无论光的强度多大,都不会观测到光电子从电极逸出。b).每个光电子的能量只与照射光的频率υ有关,而与光强度无关。光强度只影响到光电流的强度。c).当入射光频率υ>υ0时,不管光多微弱,只要光一照上,几乎立即观测到光电子。这与经典电磁理论计算结果很不一致。以上三个特点,(c)是定量上的问题,而(a),(b)在原则上无法用经典物理学来解释。⑶原子的线状光谱及规律问题到十九世纪中叶,由于光谱分析积累了相当丰富的资料,不少人对它们进行了整理与分析。1885年,巴耳末发现:氢原子可见光谱线的波数~具有下列规律)121(~22nRn=3,4,5……(4)其中R为里德堡常数。巴耳末公式与观测结果的惊人符合,引起了光谱学家的注意。紧跟着,里兹(Ritz)给出了更普遍的结合原则:每一种原子都有它特有的一系列光谱项T(n),而原子发出的光谱线的波数~总可以表成两个光谱项之差:)()(~nTmTmn(5)其中m,n是某些整数。于是,人们自然会问:原子的线状光谱产生的机制是什么?这些谱线的波长(数)为什么有这样简单的规律?光谱项的本质又是什么……⑷原子的稳定性问题。1911年,卢瑟福用α粒子去轰击原子的实验,导致了今天众所周知的“原子有核模型”。即:原子是由原子核和核外高速运动着的电子组成的。由于电子在原子核外作加速运动,而按经典电动力学的理论可知,加速运动的带电粒子将不断辐射电磁波而丧生能量。因此,围绕原子核外运动的电子,终究会因大量丧失能量而“掉到”原子核中去,这样,原子也就“崩溃”了。但现实与理论的矛盾十分尖锐地摆在面前,如...