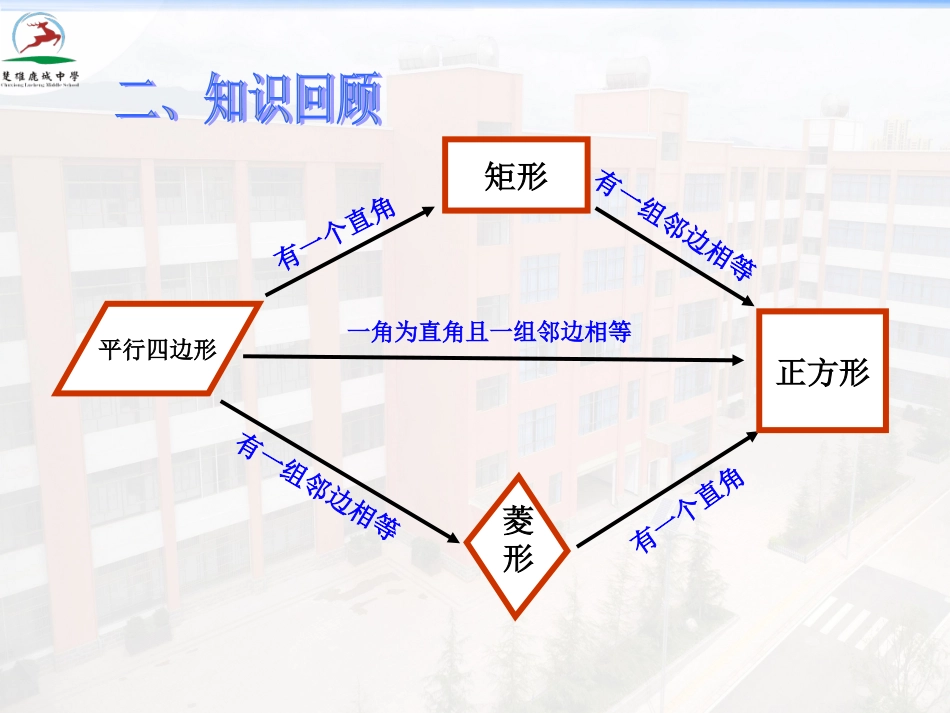
专题复习特殊四边形的证明及计算楚雄鹿城中学郑永全1、理解矩形、菱形、正方形与平行四边形的关系。2、掌握特殊四边形的有关性质及判定方法,并能应用所学知识解决相关问题。3、掌握特殊四边形的常用解题方法及思路平行四边形有一个直角矩形有一组邻边相等菱形有一组邻边相等有一个直角正方形一角为直角且一组邻边相等特殊四边形的特殊四边形的性质性质边对边平行且相等对边平行且相等对边平行四条边都相等对边平行四条边都相等角对角相等邻角互补四个角是直角对角相等邻角互补四个角是直角对角线互相平分相等且互相平分互相垂直平分每条对角线平分一组对角互相垂直平分且相等,每条对角线平分一组对角对称性中心对称图形中心对称图形轴对称图形中心对称图形轴对称图形中心对称图形轴对称图形平行四边形(1)两组对边分别平行;(2)两组对边分别相等;(3)一组对边平行且相等;(4)对角线互相平分。矩形(1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形;(3)对角线相等的平行四边形是矩形。菱形(1)有一组邻边相等的平行四边形是菱形;(2)四条边都相等的四边形是菱形;(3)对角线互相垂直的平行四边形是菱形。正方形(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;(2)有一组邻边相等的矩形是正方形;(3)有一个角是直角的菱形是正方形。特殊四边形的特殊四边形的判定方法判定方法1、对角线相等的四边形是矩形。()2、一组对边平行,另一组对边相等的四边形是平行四边形。()3、四个角相等的四边形是正方形。()4、邻角相等的平行四边形是矩形。()5、正方形的对角线相等、垂直且平分。()6、对角线垂直且平分的四边形是菱形。()7、对角线互相垂直的矩形是正方形。()8、对角线相等的菱形是正方形。()╳╳╳√√√√√1、在进行特殊四边形的计算或证明时,首先要认清研究对象,找出题目中所给的显性条件和隐性条件,重点关注研究对象特有的几何性质;2、特殊四边形的判定,关键在于掌握判定方法,对照判定条件逐条入手;3、特殊四边形的计算或证明(参考以下思路):((11)平行四边形重点利用好平行这个特性,利用平行将已知条件转化到同一)平行四边形重点利用好平行这个特性,利用平行将已知条件转化到同一个三角个三角形或有联系的两个三角形中,利用勾股定理、直角三角形或等腰三角形性质进行计算或证形或有联系的两个三角形中,利用勾股定理、直角三角形或等腰三角形性质进行计算或证明;明;((22)矩形因有四个角均为直角和对角线相等这一特性,重点考虑利用勾股定)矩形因有四个角均为直角和对角线相等这一特性,重点考虑利用勾股定理、理、等腰、等边三角形进行相关运算,以及等腰、等边三角形进行相关运算,以及30º30º、、60º60º特殊角的运用(如:特殊角的运用(如:30º30º所对直角边所对直角边等于斜边的一半);等于斜边的一半);((33)菱形因其具有四边相等、对角相等、邻角互补、对角线垂直等特性,在)菱形因其具有四边相等、对角相等、邻角互补、对角线垂直等特性,在进行进行相关运算时就充分借助性质将条件转化到等腰、等边、直角三解形中进行,尤其用好相关运算时就充分借助性质将条件转化到等腰、等边、直角三解形中进行,尤其用好30º30º、、60º60º特殊角;其次菱形的面积计算也是常考点之一,计算公式是:菱形的面积等于对角线特殊角;其次菱形的面积计算也是常考点之一,计算公式是:菱形的面积等于对角线乘积的一半;乘积的一半;((44)正方形具有平行四边形、菱形、矩形的一切性质,除了上述解题思路外,)正方形具有平行四边形、菱形、矩形的一切性质,除了上述解题思路外,正方正方形还应注意用好形还应注意用好45º45º的等腰三角形。的等腰三角形。1、如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长。.2、如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.(1)若DE=BF,求证:四边形AFCE是平行四边形;(2)若四边形AFCE是菱形求菱形AFCE的周长.3、如图,四边形ABCD是矩形,对角...