关于原点对称的点的坐标上课4VIP免费

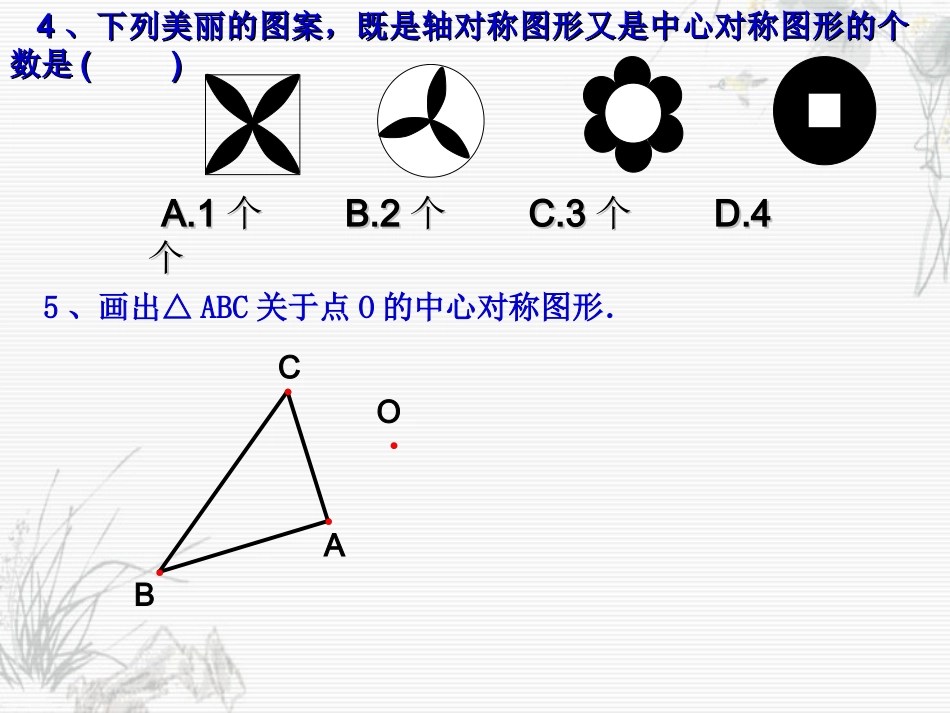
☆☆知识巩固知识巩固2、中心对称有何性质？1、什么叫中心对称和中心对称图形？把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点成中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形互相重合，那么这个图形叫做中心对称图形；这个点叫做它的对称中心；互相重合的点叫做对称点.（2）关于中心对称图形的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。（1）关于中心对称的两个图形是全等形。33、在下列图形中，是中心对称图形的是（）、在下列图形中，是中心对称图形的是（）44、下列美丽的图案，既是轴对称图形又是中心对称图形的个、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是数是()()A.1A.1个个B.2B.2个个C.3C.3个个D.4D.4个个OCBA5、画出△ABC关于点O的中心对称图形．知识引入•什么是平面直角坐标系？•怎样在平面直角坐标系内表示一个点的坐标？•点P(a,b)关于x轴的对称点的坐标是，关于y轴对称点的坐标是。填一填1.点P(2,3)关于x轴的对称点的坐_________关于Y轴的对称点的坐标是_____________.2.点M(-3,-4)在第___象限,点M到x轴的距离是_____,到Y轴的距离是_____,到原点的距离是______.yxABCDEF5-5-2-3-4-13241-55-3-44-23-121o如图，在直角坐标系中，已知A、B、C、D、E、F，作出A、B、C、D、E、F点关于原点O的中心对称点，并写出它们的坐标，并回答：这些坐标与已知点的坐标有什么关系？(0,3)(-3,1)(-4,0)(2,2)(3,-3)(-2,-2)探究探究解:A(-3,1)B(-4,0)C(0,3)D(2，2)E(3,-3)F(-2,-2)关于原点O的对称点(3,-1)(4,0)(0,-3)(-2,-2)(-3,3)(2,2)☆☆归纳归纳两个点关于原点对称时，它们的坐标符号相反，即：点P（x,y）关于原点O的对称点P/（-x,-y）．如图，利用关于原点对称的点的坐标的特点，作出与线段AB关于原点对称的图形．-3-33OBA-2-21-1yx3-44221-1☆☆例题精例题精析析B′A′即为所求。线段，连接原点的对称点分别为关于（的两个端点线段因此，关于原点的对称点为（点BABABABAAByxPyxP).0,3(),1,0()0,3),1,0(),,(),解：1．下列函数中，图象一定关于原点对称的图象是（）A．y=B．y=2x+1C．y=-2x+1D．以上三种都不可能1x3．如果点P（-3，1），那么点P（-3，1）关于原点的对称点P/的坐标是P/_______．4．写出函数y=-与y=具有的一个共同性质______．3x3x☆☆练一练练一练)2,0(),0,5(),1,2(),1,2(),5,0(),0,2(),1,2(),2,0(),0,5(.2IHGFEDCBAO对称？于原点下列各点中哪两个点关☆☆练习巩固练习巩固原点对称的图形。关于标的特点，作出关于原点对称的点的坐）利用，（）、，（、，已知ABCCBAABC1231)2,1(.1。对称，试求ｘ＋ｙ的值关于原点与点（已知点)4,1()4,2.222yxQyxP-3-33OBA-2-21-1yx3-44221-1☆☆应用拓展应用拓展如图，直线AB与x轴、y轴分别相交于A、B两点，将直线AB绕点O顺时针旋转90°得到直线A1B1．（1）在图中画出直线A1B1．（2）求出过线段A1B1中点的反比例函数解析式．（3）是否存在另一条与直线AB平行的直线y=kx+b，它与（2）中双曲线只有一个交点，若存在，求此直线的函数解析式，若不存在，请说明理由．-3-33OBA-2-21-1yx3-44221-1作业1、习题23.22、如图已知△ABC中，A(-2,3)B(-3,1)C(-1,2)。（1）将△ABC向右平移4个单位长度，画出平移后的△A1B1C1..。（2）画出△ABC关于x轴对称的△A2B2C2（3）将△ABC绕原点O旋转180度，画出旋转后的△A3B3C3（4）在△A1B1C1..、△A2B2C2、△A3B3C3中：△与△成轴对称，对称轴是；△与△成中心对称，对称中心的坐标是（，）。小结本节课你学会了什么?