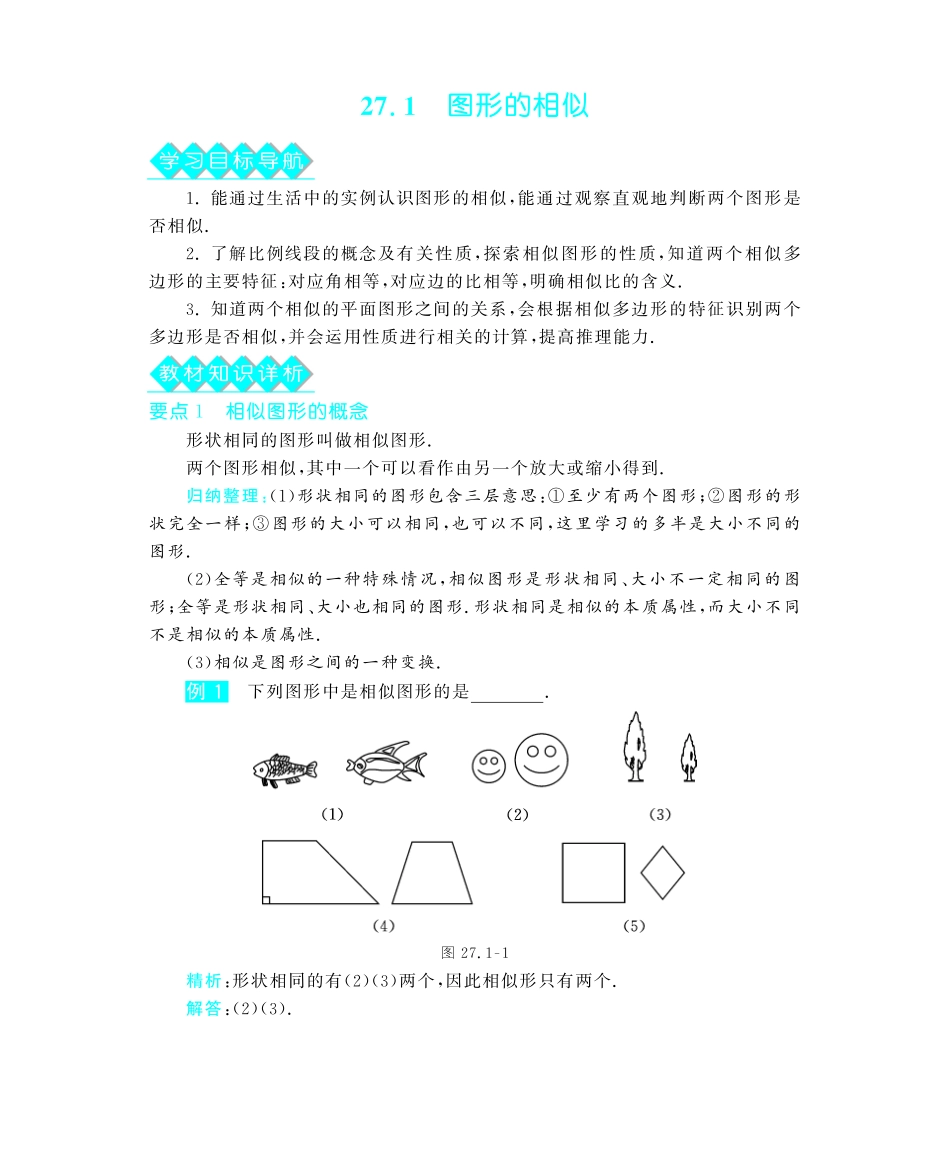
27.1图形的相似学习目标导航1.能通过生活中的实例认识图形的相似,能通过观察直观地判断两个图形是否相似.2.了解比例线段的概念及有关性质,探索相似图形的性质,知道两个相似多边形的主要特征:对应角相等,对应边的比相等,明确相似比的含义.3.知道两个相似的平面图形之间的关系,会根据相似多边形的特征识别两个多边形是否相似,并会运用性质进行相关的计算,提高推理能力.教材知识详析要点1相似图形的概念形状相同的图形叫做相似图形.两个图形相似,其中一个可以看作由另一个放大或缩小得到.归纳整理:(1)形状相同的图形包含三层意思:①至少有两个图形;②图形的形状完全一样;③图形的大小可以相同,也可以不同,这里学习的多半是大小不同的图形.(2)全等是相似的一种特殊情况,相似图形是形状相同、大小不一定相同的图形;全等是形状相同、大小也相同的图形.形状相同是相似的本质属性,而大小不同不是相似的本质属性.(3)相似是图形之间的一种变换.例1下列图形中是相似图形的是.图27.1G1精析:形状相同的有(2)(3)两个,因此相似形只有两个.解答:(2)(3).(1)由相似图形的定义可知,相似图形的实质就是“形状相同”,对于图形的大小、位置并没有要求.两个图形相似,其中的一个图形可以看做是由另一个图形放大或缩小得到的.(2)当“形状相同,大小相等”时,两个图形相似但实质上也是全等,因此,“全等”是“相似”的特殊情况.要点2比例线段在四条线段a,b,c,d中,如果a和b的比等于c和d的比,即ab=cd(a∶b=c∶d或写成ad=bc),我们就说这四条线段是成比例线段,简称比例线段.关键提醒:判断四条线段是否成比例,应先将四条线段的长度单位统一,然后将四条线段按从小到大的顺序排列,再判断前两条线段的长度比是否等于后两条线段的长度比.归纳整理:(1)在有顺序的比例式a∶b=c∶d中,d叫做a,b,c的第四比例项.(2)若a∶b=b∶c,则b2=ac,线段b叫做a,c的比例中项.(3)比例的基本性质:如果ab=cd,那么ad=bc;合比性质:若ab=cd,则a±bb=c±dd;等比性质:若ab=cd==mn(b+d++n≠0),则a+c++mb+d++n=ab.(4)把线段AB分成两条线段AC和BC(AC>BC).如果ACAB=BCAC,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.通过计算可知黄金比的比值为ACAB=BCAC=5-12,我们把这一比值叫做黄金数,它可近似等于0.618.图27.1G2例2判断下列四条线段a,b,c,d是否成比例.(1)a=4,b=6,c=5,d=10;(2)a=12,b=8,c=15,d=10.精析:只需求出a∶b和c∶d的大小进行比较即可,当比值相等时,说明四条线段成比例,当比值不相等时,说明四条线段不成比例.解答:(1)因为ab=46=23,cd=510=12,所以ab≠cd,所以a,b,c,d不成比例.(2)因为ab=128=32,cd=1510=32,所以ab=cd,所以a,b,c,d成比例.(1)求线段的比时,要先统一长度单位,即在同一长度单位下求两条线段的长度比.(2)判断四条线段是否成比例的方法:只要把四条线段按照一定的顺序排列,分别计算前两条线段和后两条线段的比是否相等即可.要点3相似多边形的性质相似多边形的对应角相等,对应边的比相等.相似多边形对应边的比等于相似比.归纳整理:(1)相似多边形中的对应三角形相似,相似比等于相似多边形的相似比.(2)相似比的值和两个多边形的前后顺序有关.(3)全等的多边形的相似比等于1,反之相似比等于1的相似多边形是全等的多边形.例3在如图27.1G3所示的相似四边形中,α比β大15°,求未知边x,y的长度和角α,β的大小.图27.1G3精析:依据相似多边形的性质:对应边的比相等,对应角相等列出方程或方程组,即可求出x,y,α和β.解答:因为两个四边形相似,它们的对应边的比相等,对应角相等,所以126=8y=x3,解得y=4,x=6.α+β+60°+115°=360°,又α=β+15°,可得α=100°,β=85°.应用相似多边形的性质时,找出相似多边形的对应边和对应角是解决此类问题的关键,一般情况下,两个多边形中最长的边与最长的边是对应边,最短的边与最短的边是对应边;最大的角与最大的角是对应角,最小的角...