北京市高考数学压轴卷 理试卷VIP免费

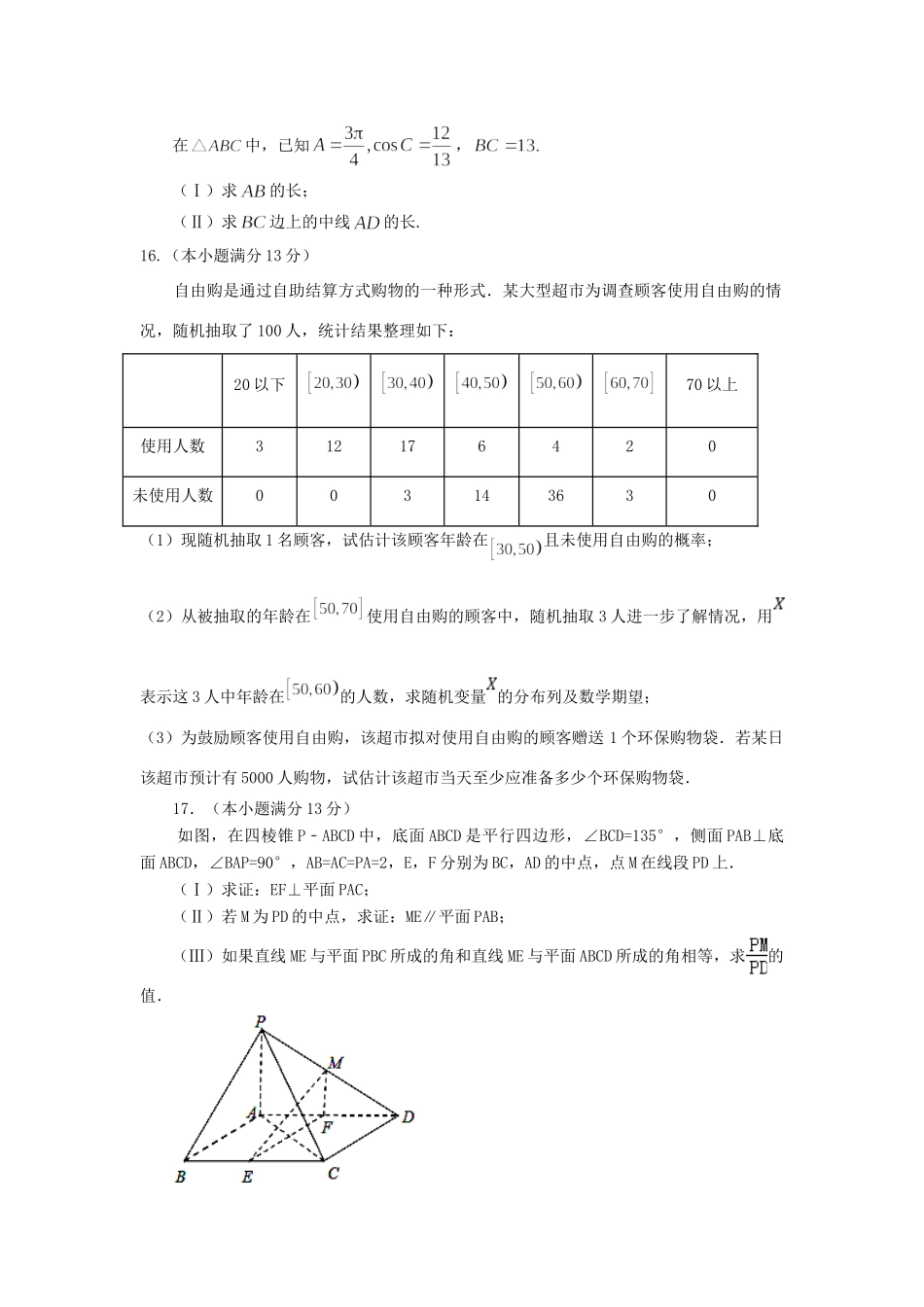
北京市2019年高考数学压轴卷理（含解析）一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。1.已知(1i)i1i(bbR)，则b的值为（）A.1B.1C.iD.i2．下列函数中，值域为R的偶函数是（）A．y=x2+1B．y=ex﹣e﹣xC．y=lg|x|D．3．若变量yx,满足约束条件2,1,0xyxy,则yxz2的最大值为（）A．0B．2C．3D．44.某程序框图如图所示，执行该程序，若输入的a值为1，则输出的a值为（）输出输入开始结束是否A.1B.2C.3D.55.某四棱锥的三视图如图所示，则该四棱锥的侧面积是（）A．27B．30C．32D．366.“4ab”是直线210xay与直线220bxy平行的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.已知点(22,0)Q及抛物线24xy上一动点(,)Pxy，则||yPQ的最小值是（）A．12B．1C．2D．38.设函数()fx的定义域D，如果存在正实数m，使得对任意xD，都有()()fxmfx，则称()fx为D上的“m型增函数”，已知函数()fx是定义在R上的奇函数，且当0x时，()fxxaa（aR）．若()fx为R上的“20型增函数”，则实数a的取值范围是（）A．0aB．5aC．10aD．20a二、填空题（本大题共6个小题，每小题5分，满分30分.把答案填在题中的横线上．）9.函数2sin(2)16yx的最小正周期是，最小值是．10．已知，且114yx，若恒成立，则实数的取值范围是__________．11.如果平面直角坐标系中的两点(1,1)Aaa，(,)Baa关于直线l对称，那么直线l的方程为．12.51xx的二项展开式中x项的系数为_________．（用数字作答）13.若，，，，则，，有小到大排列为．14.数列{}na满足：*112(1,)nnnaaannN，给出下述命题：①若数列{}na满足：21aa，则*1(1,)nnaannN成立；②存在常数c，使得*()nacnN成立；③若*(,,,)pqmnpqmnN其中，则pqmnaaaa；④存在常数d，使得*1(1)()naandnN都成立．上述命题正确的是____．(写出所有正确结论的序号)三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.（本小题满分13分）在中，已知，（Ⅰ）求的长；（Ⅱ）求边上的中线的长.16.（本小题满分13分）自由购是通过自助结算方式购物的一种形式．某大型超市为调查顾客使用自由购的情况，随机抽取了100人，统计结果整理如下：20以下70以上使用人数312176420未使用人数003143630（1）现随机抽取1名顾客，试估计该顾客年龄在且未使用自由购的概率；（2）从被抽取的年龄在使用自由购的顾客中，随机抽取3人进一步了解情况，用表示这3人中年龄在的人数，求随机变量的分布列及数学期望；（3）为鼓励顾客使用自由购，该超市拟对使用自由购的顾客赠送1个环保购物袋．若某日该超市预计有5000人购物，试估计该超市当天至少应准备多少个环保购物袋．17．（本小题满分13分）如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E，F分别为BC，AD的中点，点M在线段PD上．（Ⅰ）求证：EF⊥平面PAC；（Ⅱ）若M为PD的中点，求证：ME∥平面PAB；（Ⅲ）如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等，求的值．18.（本小题满分14分）已知函数.（Ⅰ）当时，求函数的极小值；（Ⅱ）当时，讨论的单调性；（Ⅲ）若函数在区间上有且只有一个零点，求的取值范围.19.（本小题满分14分）已知圆:O221xy的切线l与椭圆:C2234xy相交于A，B两点．（1）求椭圆C的离心率；（2）求证：OAOB；（3）求OAB面积的最大值.20.（本小题共13分）已知曲线nC的方程为：*1()nnxynN.（1）分别求出1,2nn时，曲线nC所围成的图形的面积;（2）若()nSnN表示曲线nC所围成的图形的面积，求证：()nSnN关于n是递增的;（3）若方程(2,)nnnxyznnN，0xyz，没有正整数解，求证：曲线(2,)nCnnN上任一点对应的坐标(,)xy，,xy不能全是有理数.1.【答案】A【解析】试题分析：因为（1+bi）i=i+bi2=-b+i=-1+i，所以1b，1b．2．【答案】C【解析】试题分析：y=x2+1...