山东省烟台市高三数学上学期期末统考试卷 理试卷VIP免费

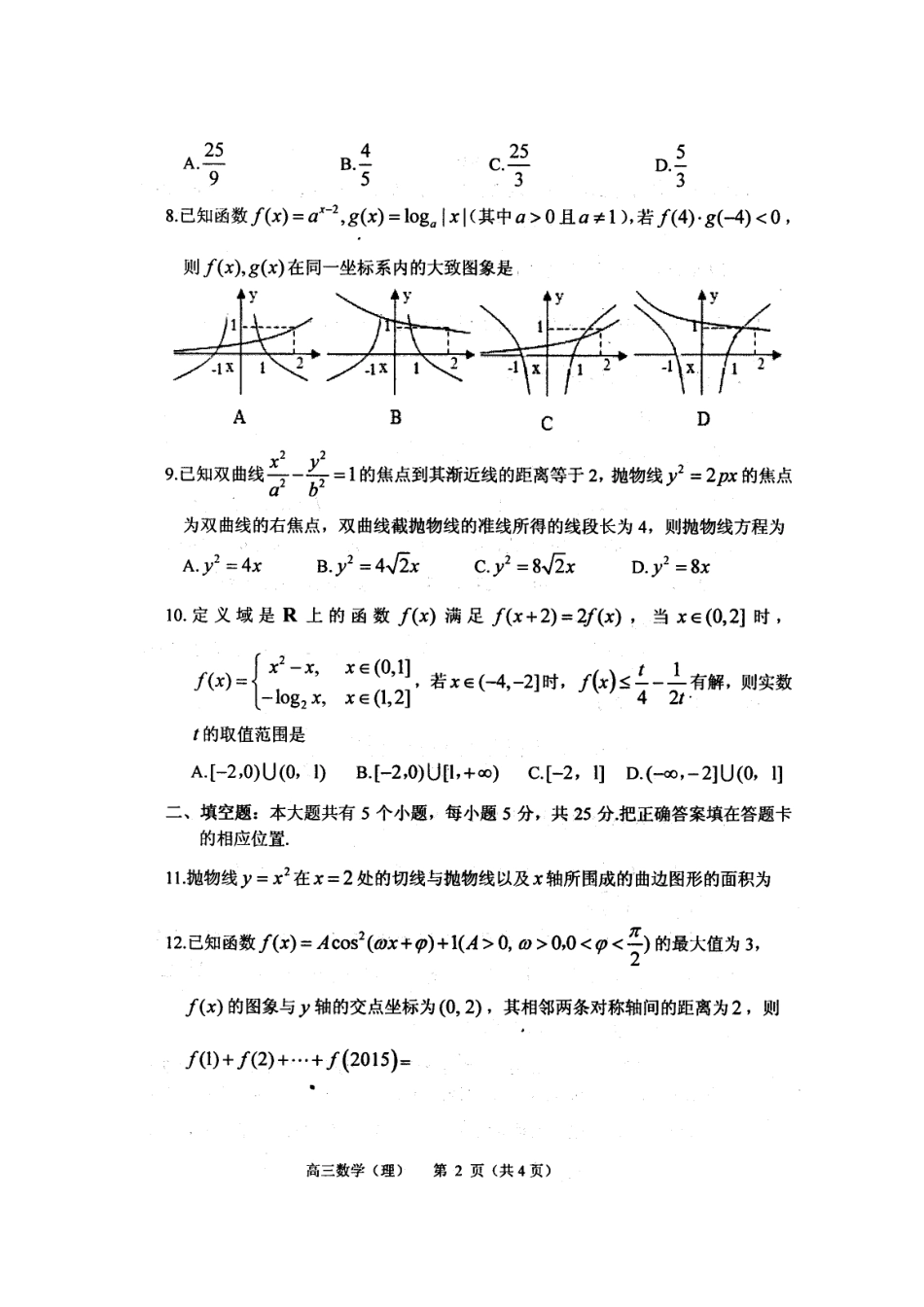
山东省烟台市2015届高三数学上学期期末统考试题理（扫描版）高三期末理科数学试题参考答案及评分标准一、选择题DBCADBABCB二、填空题11.12.403013.514.15.①④三、解答题16.解：（1）……………………3分周期，因为，所以，…………5分当，即时函数单调递减；所以的单调递减区间为.…………7分（2）当，，…………9分，当时取最大值，故当时，函数的最大值为1.…………12分17.解：（1）由题意可知，是奇函数，为偶函数，为非奇非偶函数，……………2分所以；……………4分（2）由题意可知，的所有可能取值为，……………5分，，，，………9分所以的分布列为：1234P所以.………12分18.解：（1）设AC，BD交于O，取EB中点G，连结FG，GO，在BDE中，，即四边形FAOG是平行四边形.………2分//,FGAO又AO平面EFB，FG平面EFB，所以直线AC//平面EFB.………4分（2）因为平面，所以与平面所成角就是，又与平面所成角的正切值为，所以，而，所以.………………6分分别以DA，DC，DE所在的直线为,,xyz轴，建立空间直角坐标系，则有,,,,设为平面AEB的一个法向量，则，即，不妨设，可得平面AEB的一个法向量………9分设平面FBE的一个法向量，则，令，可得平面的一个法向量………11分设二面角F-BE-A的大小为，，所以二面角F-BE-A的大小为6.………12分19.解：（1）令可得，即，所以，…1分，可得，当成立，………………………3分当时，两边相乘可得，所以，………………………5分显然当时，满足上式，所以数列是等差数列，其通项公式为.………………………6分（2）由（1）可知，从而可得，………………………7分，………………………9分因为均大于0，所以，………10分而是关于的增函数，所以，所以，故.………………………12分20.解：（1），……………………………………1分由导数的几何意义可知，，所以切线方程为：，即.………………………………………………3分（2），（其中），………4分当时，在上，此时在单调递增，当时，在上，此时在单调递减，在上，此时在单调递增；……………7分综上所述：当时，在单调递增；当时，在单调递减，在单调递增.………………8分（3）当时，，不等式为，即，只需小于（）的最小值即可，………10分由（2）可知，在单调递减，在单调递增，所以当时，，………12分故，可得，所以的取值范围为.………13分21.解：（1）由可得，，①可得，，…2分在中由余弦定理有，，又，可得②，…………………………4分联立①②得，所以椭圆方程为.…………………………6分（2）设点，由，得，…………………………8分，化简得，所以，………………………10分所以.由，得，假设存在点，坐标为，则，，…………………12分因为以为直径的圆恒过点，所以，即，所以有对任意的都成立，则，解得，故存在定点符合题意.…14分