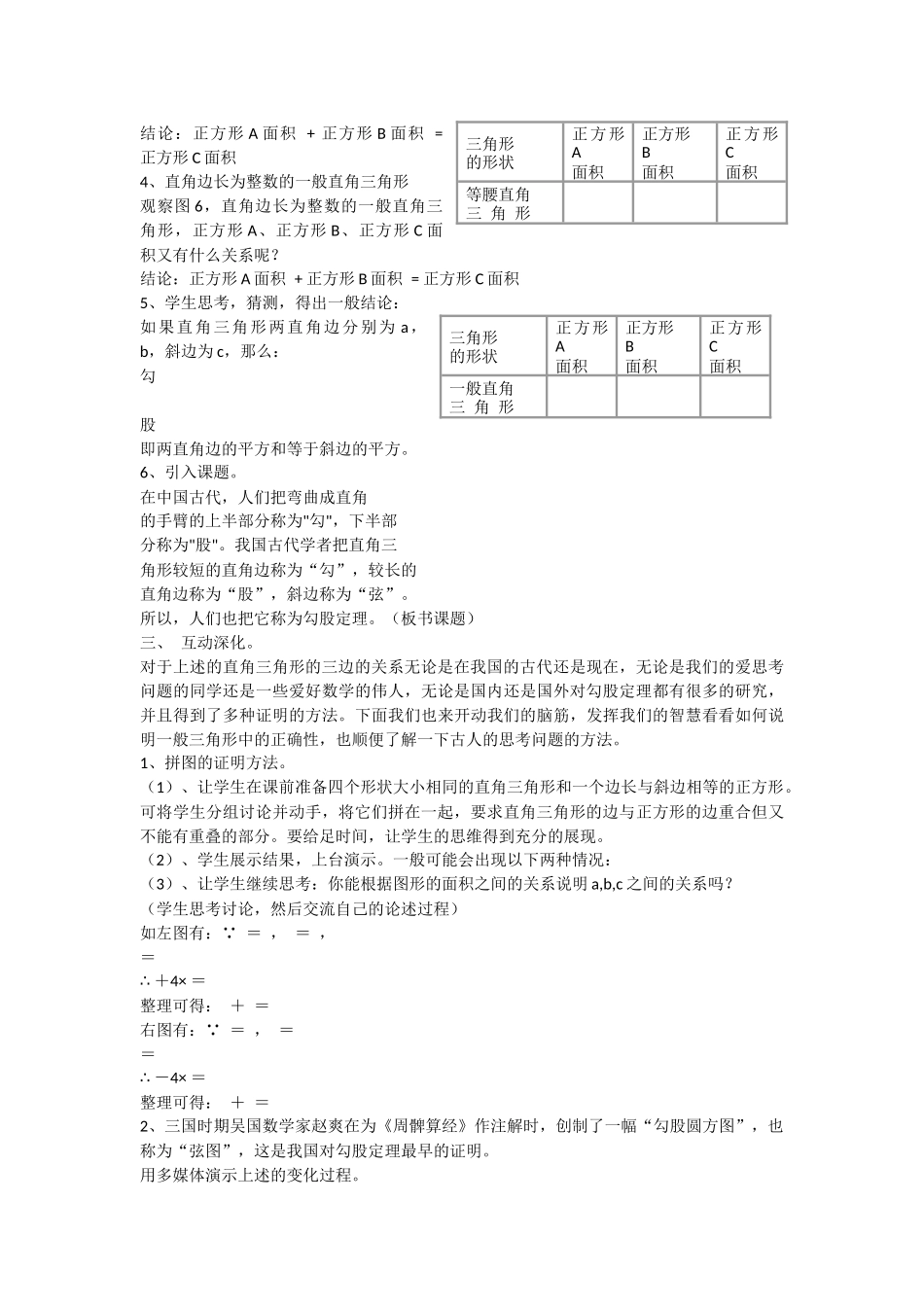
教材分析:勾股定理是中国几何的根源。古代数学家常以勾股形代替一般三角形进行研究,从而可以避开角的性质的研讨和不触及平行的烦琐理论,使几何体系简洁明了,问题的解法更加精致。本节是直角三角形相关知识的延续,同时也是学生认识无理数的基础,充分体现了数学知识承前启后的紧密相关性、连续性。勾股定理是直角三角形的重要性质,它把三角形有一个直角的“形”的特点,转化为三边之间的“数”的关系,它是数形结合的典范。它可以解决许多直角三角形中的计算问题,它是直角三角形特有的性质,是初中数学教学内容重点之一。此外,历史上勾股定理的发现反映了人类杰出的智慧,其中蕴涵着丰富的科学与人文价值。教学目标:知识技能:了解勾股定理的文化背景,体验勾股定理的探索过程。数学思考:在勾股定理的探索过程中,发展合情的推理能力,体会数形结合的思想。解决问题:1.通过拼图等活动,体验数学思维的严谨性,发展形象思维。2,在探究活动中,学会与人合作并能与他人交流思维的过程和探究的结果。3.能用勾股定理解决一些生活中的简单的问题。情感态度:1,通过对勾股定理的了解,感受数学文化,激发学习热情。2,在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神。教学重点、难点重点:用面积法探索勾股定理,理解并掌握勾股定理。难点:勾股定理的探索及证明。教学过程一、创设情境.(师)请同学们观察动画,我国科学家曾向太空发射勾股图试图与外星人沟通,在2002年的国际数学家大会上采用弦图作为会标,它为什么有如此大的魅力呢?它蕴涵着怎样迷人的奥妙呢?这节课我就带领大家一起探索勾股定理。(设计意图:用一段生动有趣的动画,点燃学生的求知欲,以景激情,以情激思,引领学生进入学习情境。)二、启发探究1、(师)问题:小明是一个爱思考问题的同学,一次在自家玩耍时,看着家里的地面砖,并从中发现了直角三角形的某种关系,同学们,你知道他看出了什么问题吗?我们也来看看,看能不能发现什么?2、(观察图1)你知道正方形C的面积是多少吗?你是怎样得出上面结果的呢?(生)独立思考后交流,采用直接数方格的办法,或者运用面积的和差计算正方形C的面积。(多媒体演示)3、观察思考,等腰直角三角形观察图5,对于等腰直角三角形,将正方形A、正方形B和正方形C的面积填入下表,它们的面积有什么关系?结论:正方形A面积+正方形B面积=正方形C面积4、直角边长为整数的一般直角三角形观察图6,直角边长为整数的一般直角三角形,正方形A、正方形B、正方形C面积又有什么关系呢?结论:正方形A面积+正方形B面积=正方形C面积5、学生思考,猜测,得出一般结论:如果直角三角形两直角边分别为a,b,斜边为c,那么:勾股即两直角边的平方和等于斜边的平方。6、引入课题。在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。所以,人们也把它称为勾股定理。(板书课题)三、互动深化。对于上述的直角三角形的三边的关系无论是在我国的古代还是现在,无论是我们的爱思考问题的同学还是一些爱好数学的伟人,无论是国内还是国外对勾股定理都有很多的研究,并且得到了多种证明的方法。下面我们也来开动我们的脑筋,发挥我们的智慧看看如何说明一般三角形中的正确性,也顺便了解一下古人的思考问题的方法。1、拼图的证明方法。(1)、让学生在课前准备四个形状大小相同的直角三角形和一个边长与斜边相等的正方形。可将学生分组讨论并动手,将它们拼在一起,要求直角三角形的边与正方形的边重合但又不能有重叠的部分。要给足时间,让学生的思维得到充分的展现。(2)、学生展示结果,上台演示。一般可能会出现以下两种情况:(3)、让学生继续思考:你能根据图形的面积之间的关系说明a,b,c之间的关系吗?(学生思考讨论,然后交流自己的论述过程)如左图有: =,=,=∴+4×=整理可得:+=右图有: =,==∴-4×=整理可得:+=2、三国时期吴国数学家赵爽在为《周髀算经》作注解时,创制了一幅“勾股圆方图”,也称为...