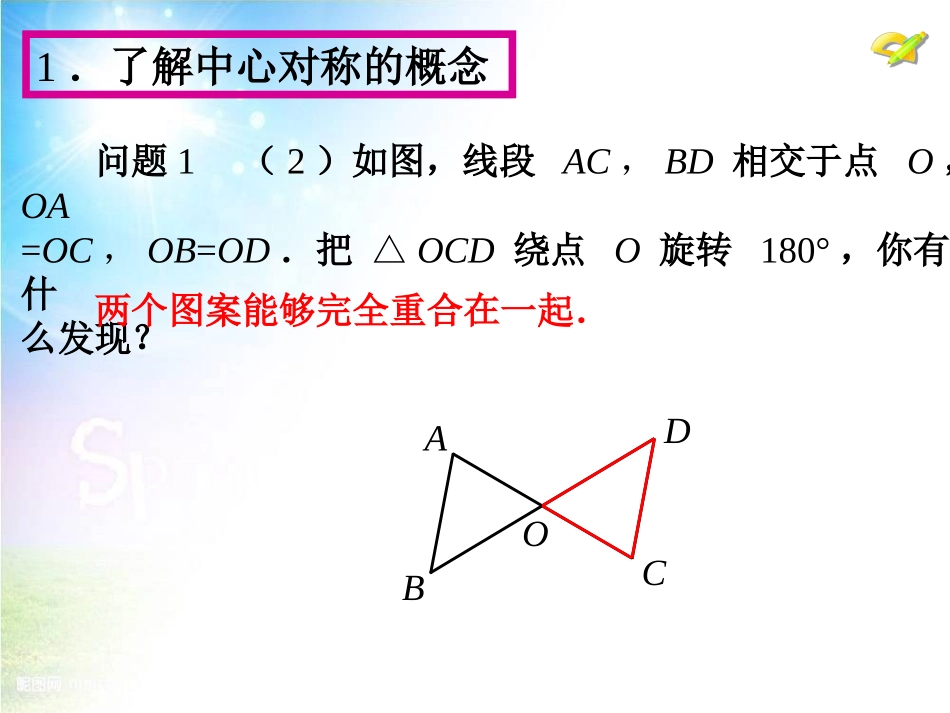
23.2中心对称(第1课时)九年级上册1.了解中心对称的概念问题1(1)如图,把其中一个图案绕点O旋转180°,你有什么发现?两个图案能够完全重合在一起.问题1(2)如图,线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现?1.了解中心对称的概念两个图案能够完全重合在一起.ABDCO问题2你能说说上述两个旋转的共同点吗?(1)图形中旋转中心是哪一点?(2)旋转的角度是多少?(3)两个图形的关系?1.了解中心对称的概念(点O)(180°)(重合)像这样,把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.这个点叫做对称中心.这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.1.了解中心对称的概念问题3中心对称与一般的旋转的联系和区别?联系:中心对称和一般的旋转都是绕着某一点进行旋转;区别:中心对称的旋转角度都是180°,一般的旋转的旋转角度不固定,中心对称是特殊的旋转.1.了解中心对称的概念CABC'A′B′O2.探究中心对称的性质问题5中心对称是特殊的旋转,它有哪些性质?画好图形后思考:(1)点O在线段AA'上吗?如果在,在什么位置?(2)△ABC和△ABC有什么关系?(3)你能从这个探究中得到什么结论?'''(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;(2)中心对称的两个图形是全等图形.2.探究中心对称的性质AA′B′BO•2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法灵活运用,体会内涵以点以点OO为对称中心为对称中心,,作出点作出点AA的对称点的对称点A′;A′;以点以点OO为对称中心为对称中心,,作出线段作出线段ABAB的对称线段点的对称线段点A′B′A′B′点点A′A′即为所求的点即为所求的点例例11(2)(2)如图如图23.2-5,23.2-5,选择点选择点OO为对称中心为对称中心,,画出与画出与△△ABCABC关于点关于点OO对称的△对称的△A′B′C′.A′B′C′.A′A′C′C′B′B′△△A′B′C′A′B′C′即为所求的三角形。即为所求的三角形。例1(3)已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。ABA’C’B’D’DOC四边形四边形AA11BB11CC11DD11即为所求的图形。即为所求的图形。画一个与已知四边形ABCD中心对称图形。(1)以顶点A为对称中心;(2)以BC边的中点为对称中心。提高练习DABCEFGMDABCO.N•如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。ABCA’B’C’•解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)ABCA’B’C’OO•解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。ABCA’B’C’