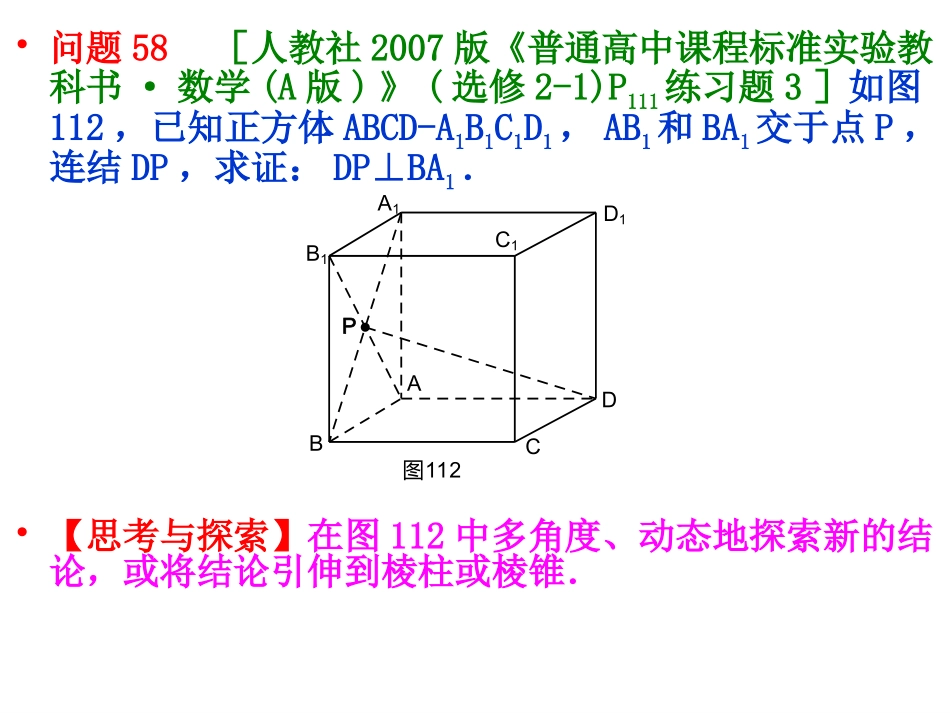
追溯湖北高考十年自主命题立体几何命题之奥秘—兼谈探究性学习武汉经济技术开发区何文桂特级教师工作室2013.9•高考年年考,试题年年新,可谓是“神秘莫测”!果真如此吗?下面我们一起追溯湖北高考十年自主命题立体几何命题之奥秘,并以此说明引导学生探究性学习的重要性!•问题58[人教社2007版《普通高中课程标准实验教科书·数学(A版)》(选修2-1)P111练习题3]如图112,已知正方体ABCD-A1B1C1D1,AB1和BA1交于点P,连结DP,求证:DP⊥BA1.•【思考与探索】在图112中多角度、动态地探索新的结论,或将结论引伸到棱柱或棱锥.PABCDA1B1C1D1图112作PF⊥AB于F,则∠PDF为PD与底面AC所成的角.求PD与底面AC所成角的正切值,则为2008上海卷文理科题16,12分.∠APD为二面角A-BA1-D的平面角.F图112(1)D1C1B1A1DCBAPPABCDA1B1C1D1图112当ABCD-A1B1C1D1是底面ABCD为任意四边形的直棱柱时,作AN⊥BD于N,取BN的中点Q.则PQ⊥AB,∠APN为二面角A-BA1-N的平面角.把∠BAD设为120°,再把四棱锥A1-ABCD从直四棱柱中移出来命题,则为2010湖北卷理科题18,12分.连AC交BD于Q,连B1C,A1D,则PQ∥B1C∥A1D,B1C∥平面BDP,A1D∥平面APQ,PQ∥平面B1BC∥平面A1AD,PQ∥平面A1B1CD,∠PQB为异面直线B1C与BD所成的角.因AB⊥A1D,所以PQ⊥AB.QN图112(3)D1C1B1A1DCBAPQ图112(2)D1C1B1A1DCBAPH把112(2a)正方体中的两个相邻的面ABB1A1、ABCD移出来命题,则为2002全国新课程卷文理科题19,12分.由此可得到比标准答案更直观的解法.PABCDA1B1图112(2b)Q当点P、Q分别在A1B、AC上变动时,若A1P=AQ,PQFE仍为矩形,且AE+AF=AD.因AE+AF=AD=a为定值,所以当AE=AF即E、F分别为AA1、AD的中点也即P、Q分别为A1B、AC的中点时,PQ最短.此时取PQ的中点H,则∠AHB为二面角A-PQ-B的平面角.在图112(2)中,作PE⊥AA1于E,QF⊥AD于F,则PQFE为矩形,且E、F分别为AA1、AD的中点.EFFEQ图112(2a)D1C1B1A1DCBAPPABCDA1B1C1D1图112(2)Q异面直线CP与D1Q所成角的余弦值为-16.当M为DD1的中点时,平面APQ⊥平面MPQ,且MQ⊥DC1.由此可将正方体改为正四棱柱ABCD-A1B1C1D1,当M在DD1的何处时平面APQ⊥MPQ平面进行命题.MP图112(2c)D1C1B1A1DCBAQ设R、O分别是面AD1、体AC1的中心,则O-PQR为OP、OQ、0R两两互相垂直的正三棱锥,其体积是正方体体积的148,全面积是正方体全面积的3+348.取PQ的中点H,则∠BHC1,∠BHD1,∠AHB,∠AHC1,∠AHD1分别为二面角B-PQ-C1,B-PQ-D1,A-PQ-B,A-PQ-C1,A-PQ-D1的平面角.ROQ图112(5)D1C1B1A1DCBAPHQ图112(4)D1C1B1A1DCBAP将C改为BC上任一点M时,该结论仍成立.如果取BC的中点M,再把四棱锥A1-ABMD从正方体中移出来命题,则为2006浙江卷文理科题19,14分.作PG∥BC交A1C于G,则BA1⊥平面APGD,且∠BDP为直线BD与平面APGD所成的角F作PE⊥A1C于E,因A1C⊥AP,所以A1C⊥平面APE,∠AEP为二面角A-A1C-B的平面角.A1D∥平面APC;作PF⊥AB于F,则∠PCF为直线CP与底面AC所成的角.把四棱锥A1-ABCD从正方体中移出来命题,则为2004天津卷文理科题19,12分.EMGE图112(8)D1C1B1A1DCBAPG图112(7)D1C1B1A1DCBAP图112(6)D1C1B1A1DCBAP因为AC⊥PM于,设E为BM的中点,在AB上确定一点N,使EN⊥PM,并求EN与平面NPM所成角的正切值.此即为2012湖北卷理科题19(12分)(2).因为AP⊥BA1,AD⊥平面ABB1A1,所以AD上除点A外任一点与点P的连线都垂直于BA1.取AD中点M,则PM⊥BA1,PM⊥AC.设AC交BM于R,作RT∥PM交BA1于,则RT为异面直线AC与BA1的公垂线.NEM图112(10)D1C1B1A1DCBAPRTM图112(9)D1C1B1A1DCBAPBD⊥平面A1CA内任何一条直线.∠A1CA为直线A1C与底面ABCD所成的角.易知tanθtanφ=1.反之,当ABCD-A1B1C1D1为正四棱柱时,在AA1上取点Q,设二面角A-BQ-D为θ,直线QD与底面ABCD所成角为φ,若tanθtanφ=1,则AQ=AB.把四棱锥A1-ABCD从正四棱柱中移出来命题,则为2009湖北卷理科题18,12分.作AQ⊥PD于Q,则∠ABQ为直线AB与平面DBA1所成的角.易知sinφ=22sinθ,由θ的范围可确定φ的范围.此关系式对于ABB1A1-DCC1D1为正四棱柱也成立.把三棱锥D-ABA1从正四棱柱ABB1A1-DCC1D1中移出来命题,则为2...