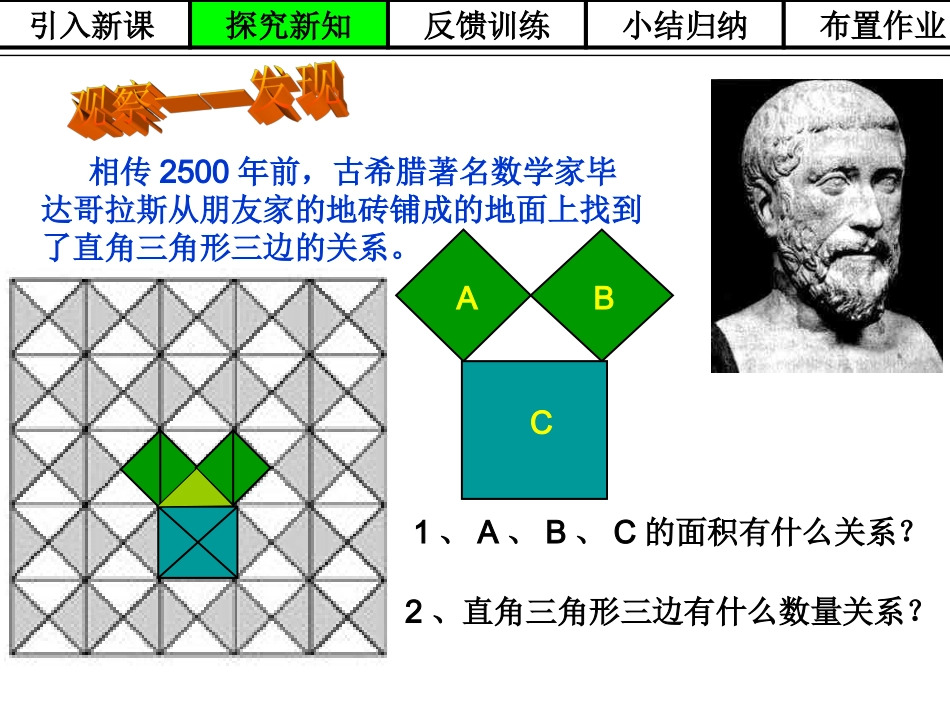
18.118.1勾股定理(勾股定理(11))人教版八年级数学(下)老河口市七中杨梅引入新课探究新知小结归纳反馈训练布置作业相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了直角三角形三边的关系。ABC引入新课探究新知小结归纳反馈训练布置作业1、A、B、C的面积有什么关系?2、直角三角形三边有什么数量关系?ABC网格中的直角三角形是否也具有这种性质?(网格中每个小方格的面积都是1)正方形A的面积正方形B的面积正方形C的面积16259引入新课探究新知小结归纳反馈训练布置作业ABC网格中的直角三角形是否也具有这种性质?正方形A的面积正方形B的面积正方形C的面积16259引入新课探究新知小结归纳反馈训练布置作业ABC网格中的直角三角形是否也具有这种性质?(网格中每个小方格的面积都是1)正方形A的面积正方形B的面积正方形C的面积16259引入新课探究新知小结归纳反馈训练布置作业ABC网格中的直角三角形是否也具有这种性质?(网格中每个正方形的边长都是1)正方形A的面积正方形B的面积正方形C的面积16259引入新课探究新知小结归纳反馈训练布置作业ABC图3-1ABC图3-2引入新课探究新知小结归纳反馈训练布置作业正方形A的面积正方形B的面积正方形C的面积命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。cab引入新课探究新知小结归纳反馈训练布置作业y=0abcbcbcbcaaa尝试用下面四个全等的直角三角形围成一个正方形动动手acbabc思考:大正方形面积怎么求?证法一:abcabcbacabcabcabcabcabc思考:大正方形面积怎么求?证法二:aabbcc伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。∟∟∟证法三:你还想知道勾股定理的其它证法吗?请上网查询,你一定会有精彩的发现。勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么222abc即直角三角形两直角边的平方和等于斜边的平方。abcy=0证明结论得到定理经过证明被确认正确的命题叫做经过证明被确认正确的命题叫做定理定理..两千多年前,古希腊有个哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾股世界勾股世界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。例题讲解引入新课探究新知小结归纳反馈训练布置作业1.求出下列直角三角形中未知边的长度68x5x13ACBACB引入新课探究新知小结归纳反馈训练布置作业815A49B251.求下列图中字母所代表的正方形的面积:引入新课探究新知小结归纳反馈训练布置作业2、已知RtABC△中,C=90∠0,BC=a,AC=b,AB=c•已知:a=1,b=2,则c=;•已知:a=6,c=10,则b=;•已知:c=13,b=12,则a=;3、如图,一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为()A.3米B.4米C.5米D.6米34引入新课探究新知小结归纳反馈训练布置作业4、如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?9m24m?引入新课探究新知小结归纳反馈训练布置作业引入新课探究新知小结归纳反馈训练布置作业...