三角形中位线课件VIP免费

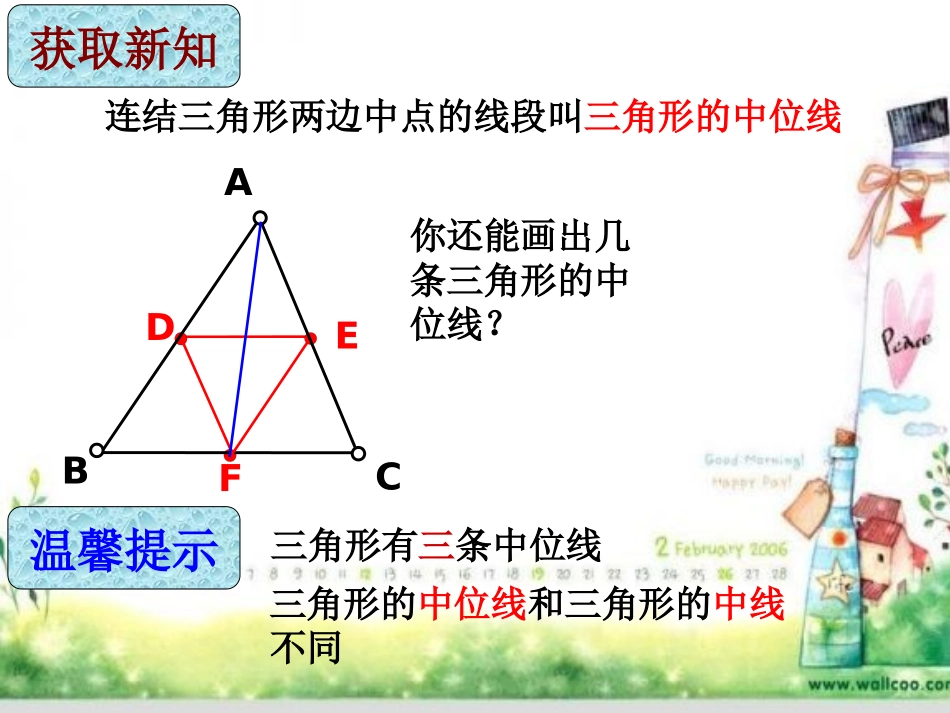
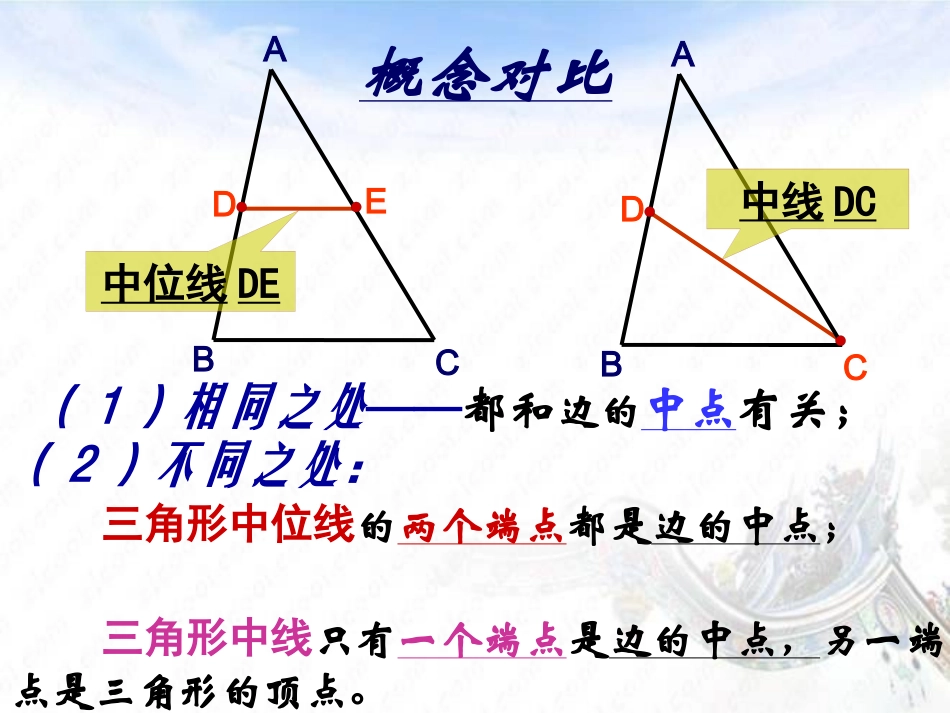
三角形的中三角形的中位线位线三角形的中位线三角形的中位线温馨提示连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线三角形的中位线和三角形的中线不同EDFACB获取新知你还能画出几条三角形的中位线？（1）相同之处——都和边的中点有关；（2）不同之处：三角形中位线的两个端点都是边的中点；三角形中线只有一个端点是边的中点，另一端点是三角形的顶点。CBAED概念对比CBAD中线DC中位线DE观察猜想在△ABC中，中位线DE和边BC什么关系?DE和边BC关系数量关系：位置关系：DEBC∥ABCDEDE=BC.21结论：三角形的中位线平行于第三边，并且等于它的一半.DABCE如图：在△ABC中，D是AB的中点，E是AC的中点。则有：DEBC,∥DE=BC.21能说出理由能说出理由吗吗??三角形的中位线的性质三角形的中位线的性质三角形的中位线平行于第三边，并且等于它的一半用符号语言表示DABCE DE是△ABC的中位线∴DEBC∥，DE=BC.21ACBEDF初试身手练习1.如图，在△ABC中，D、E分别是AB、AC的中点①若∠ADE=65°，则∠B=度，为什么？②若BC=8cm，则DE=cm，为什么？654③若AC=4cm,BC=6cm，AB=8cm，则△DEF的周长=______练习1.如图，在△ABC中，D、E、F分别是AB、AC、BC的中点9cm④若△ABC的周长为24，△DEF的周长是_____121、三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系？探究活动2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系？⑤图中有_____个平行四边形⑥若△ABC的面积为24，△DEF的面积是_____3366设计方案：F（中点）(中点)DE(中点)ABC1、三角形三条中位线围成的三角形的周长是原三角形的周长的一半。2、三角形三条中位线围成的三角形的面积与原三角形的面积的41已知：如果，点D、E、F分别是△ABC的三边的中点．（（11）若）若AB=8cmAB=8cm，求，求EFEF的长；的长；（（22）若）若DE=5cmDE=5cm，求，求BCBC的长．的长．（（33）若增加）若增加MM、、NN分别分别BDBD、、BFBF的中的中点，问点，问MNMN与与ACAC有什么关系？为什么？有什么关系？为什么？大显身手定理应用已知：在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是DC的中点，N是AB的中点．求证：∠PMN＝∠PNM．已知：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点.猜想四边形EFGH的形状并证明。ABCDEFGHE，F是AB，BC的中点，你联想到什么？要使EF成为一个三角形的中位线应怎样添加辅助线？证明：如图，连接AC EF是△ABC的中位线AC21//EF同理得：AC21//GHEF//GH∴四边形EFGH是平行四边形典例示范答：四边形EFGH为平行四边形。（1）顺次连结平行四边形各边中点所得的四边形是什么？（2）顺次连结菱形各边中点所得的四边形是什么？平行四边形矩形（3）顺次连结矩形各边中点所得的四边形是什么？菱形菱形（6）顺次连结等腰梯形各边中点所得的四边形是什么？菱形平行四边形（5）顺次连结梯形各边中点所得的四边形是什么？（4）顺次连结正方形各边中点所得的四边形是什么？正方形结论原四边形两条对角线连接四边中点所得四边形互相垂直矩形相等菱形互相垂直且相等正方形既不互相垂直也不相等平行四边形实际上，顺次连接四边形各边中点所得到的四边形一定是平行四边形，但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等，与是否互相平分无关.它的对角线是否垂直或者是否相等它的对角线是否垂直或者是否相等例1求证三角形的一条中位线与第三边上的中线互相平分．图24.4.3已知：如图所示，在△ABC中，AD＝DB，BE＝EC，AF＝FC．求证：AE、DF互相平分．证明连结DE、EF． AD＝DB，BE＝EC，∴DE∥AC（三角形的中位线平行于第三边并且等于第三边的一半）．同理EF∥AB．∴四边形ADEF是平行四边形．∴AE、DF互相平分（平行四边形的对角线互相平分）．例2如图，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．求证：31ADGDCEGE图24.4.4证明:连结ED， D、E分别是边BC、AB的中点，∴DE∥AC，21ACDE（三角形的中位线平行于第三边并且等于第三边的一半），∴△ACG∽△DEG，∴21ACDEAGGDGCGE∴31ADGDCEGE图24.4.4图24.4.5如果在图24．4．4中，取AC的中点F，假设B...