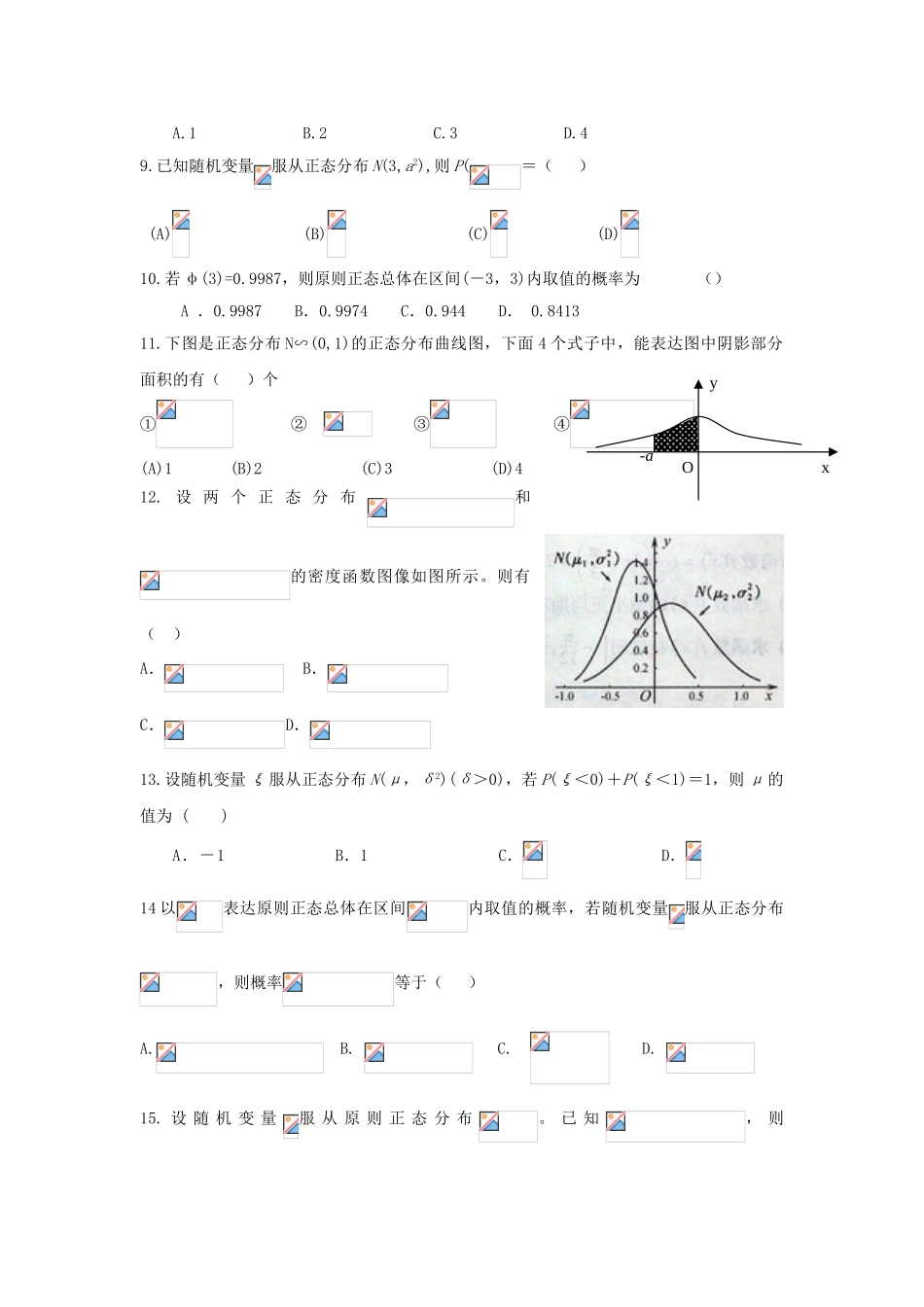
正态分布1.设随机变量服从原则正态分布,若,则()A.B.C.D.2.设随机变量,且,则c等于()3.设的概率密度函数为,则下列结论错误的是()(A)(B)(C)的渐近线是(D)~4.设随机变量服从正态分布,记,则下列结论不对的的是()A.B.C.D.5.设随机变量,且,则=()6.如果随机变量,,那么()7.已知随机变量服从正态分布,,则()A.B.C.D,8.设随机变量服从正态分布,若,则c=()A.1B.2C.3D.49.已知随机变量服从正态分布N(3,a2),则P(=()(A)(B)(C)(D)10.若φ(3)=0.9987,则原则正态总体在区间(-3,3)内取值的概率为()A.0.9987B.0.9974C.0.944D.0.841311.下图是正态分布N∽(0,1)的正态分布曲线图,下面4个式子中,能表达图中阴影部分面积的有()个①②③④(A)1(B)2(C)3(D)412.设两个正态分布和的密度函数图像如图所示。则有()A.B.C.D.13.设随机变量ξ服从正态分布N(μ,δ2)(δ>0),若P(ξ<0)+P(ξ<1)=1,则μ的值为()A.-1B.1C.D.14以表达原则正态总体在区间内取值的概率,若随机变量服从正态分布,则概率等于()A.B.C.D.15.设随机变量服从原则正态分布。已知,则yO-ax()A.0.025B.0.050C.0.950D.0.97516.分别求正态总体在,,,内取值的概率17.已知正态总体,(1)求取值不大于3的概率;(2)求取值的绝对值不不不大于3的概率.18、若~N(0,1),且令φ(x)=P(≤x),判断下列等式与否成立:(1)φ(-x)=1-φ(x);(2)P(||≤x)=1-2φ(x);(3)P(||≤x)=2φ(x)-1;(4)P(||>x)=2[1-φ(x)]。19.设,试求:(1);(2);(3)20.在某项测量中,测量成果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为________.21.A、B两个投资项目的利润率分别为随机变量X1和X2。根据市场分析,X1和X2的分布列分别为X15%10%X22%8%12%P0.80.2P0.20.50.3(1)在A、B两个项目上各投资100万元,Y1和Y2分别表达投资项目A和B所获得的利润,求方差DY1、DY2;(2)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表达投资A项目所得利润的方差与投资B项目所得利润的方差的和。求f(x)的最小值,并指出x为什么值时,f(x)取到最小值。(注:D(aX+b)=a2DX)