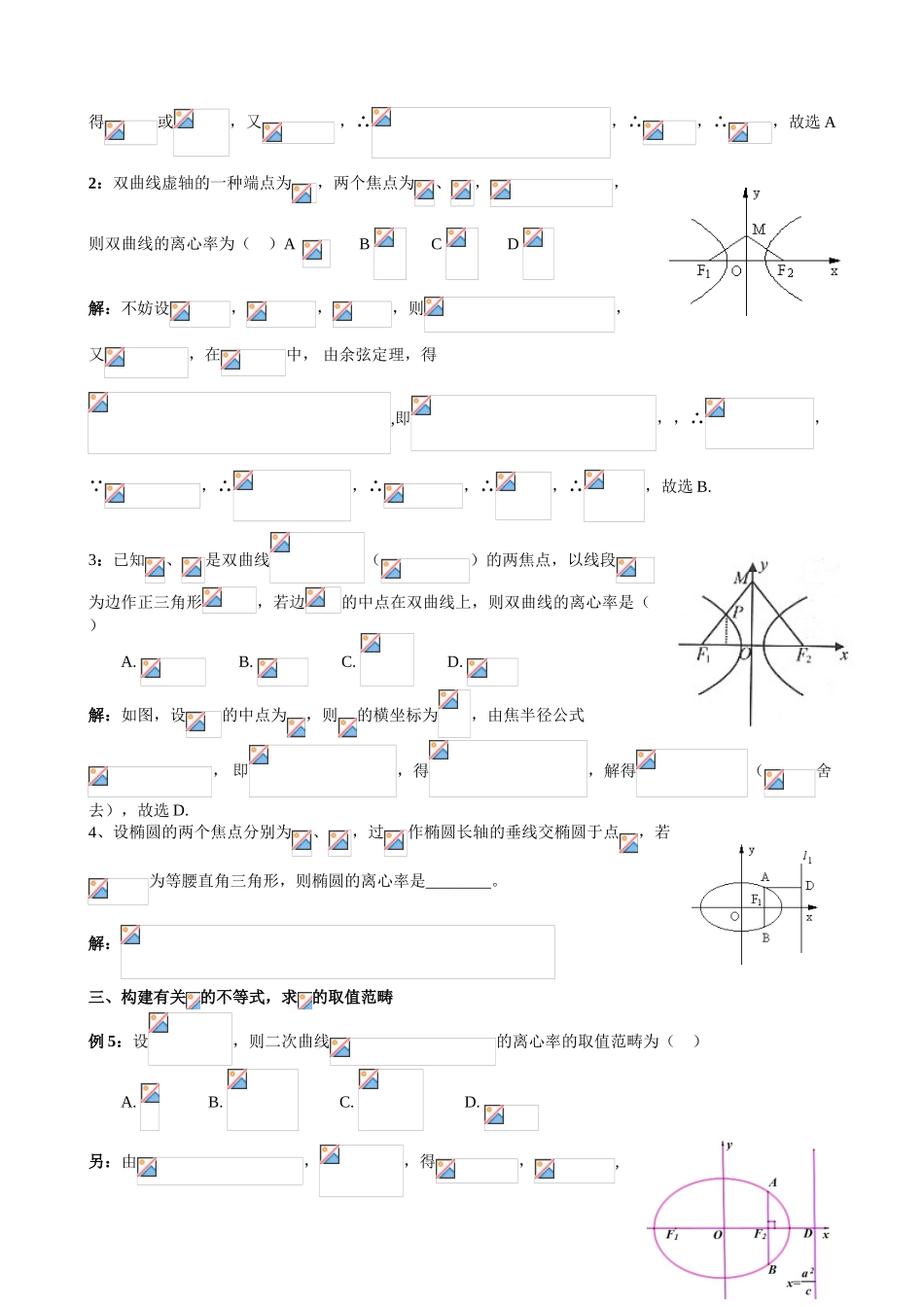
求离心率练习注意:椭圆的离心率,双曲线的离心率,抛物线的离心率.一、直接求出、,求解已知圆锥曲线的原则方程或、易求时,可运用率心率公式来解.1、如果双曲线的实半轴长为2,焦距为6,那么双曲线的离心率为()A.B.C.D解:由题设,,则,,因此选C.2、在给定椭圆中,过焦点且垂直于长轴的弦长为,,则该椭圆的离心率为()ABCD解:3、若椭圆通过原点,且焦点为、,则其离心率为()A.B.C.D.解:由、知,∴,又 椭圆过原点,∴,,∴,,因此离心率.故选C.二、构造、的齐次式方程,解出.根据题设条件,借助、、之间的关系,构造、的关系(特别是齐二次式),进而得到有关的一元方程,从而解得离心率.1:设双曲线()的半焦距为,直线过,两点.又已知原点到直线的距离为,则双曲线的离心率为()A.B.C.D.解:由已知,直线的方程为,由点到直线的距离公式,得,又,∴,两边平方,得,整顿得,得或,又,∴,∴,∴,故选A2:双曲线虚轴的一种端点为,两个焦点为、,,则双曲线的离心率为()ABCD解:不妨设,,,则,又,在中,由余弦定理,得,即,,∴, ,∴,∴,∴,∴,故选B.3:已知、是双曲线()的两焦点,以线段为边作正三角形,若边的中点在双曲线上,则双曲线的离心率是()A.B.C.D.解:如图,设的中点为,则的横坐标为,由焦半径公式,即,得,解得(舍去),故选D.4、设椭圆的两个焦点分别为、,过作椭圆长轴的垂线交椭圆于点,若为等腰直角三角形,则椭圆的离心率是________。解:三、构建有关的不等式,求的取值范畴例5:设,则二次曲线的离心率的取值范畴为()A.B.C.D.另:由,,得,,∴,∴ ,∴,∴,∴,故选D.例6:如图,已知梯形中,,点分有向线段所成的比为,双曲线过、、三点,且以、为焦点.当时,求双曲线离心率的取值范畴。解:以的垂直平分线为轴,直线为轴,建立如图所示的直角坐标系,则轴.由于双曲线通过点、,且以、为焦点,由双曲线的对称性知、有关轴对称.依题意,记,,,其中为双曲线的半焦距,是梯形的高.由定比分点坐标公式得,,设双曲线的方程为,则离心率,由点、在双曲线上,因此,将点的坐标代入双曲线方程得①将点的坐标代入双曲线方程得②再将①、②得,∴③④将③式代入④式,整顿得,∴,由题设得:,解得,因此双曲线的离心率的取值范畴为配套练习1.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于()A.B.C.D.2.设双曲线()的离心率为,且与抛物线的准线重叠,则此双曲线的方程为()A.B.C.D.3.已知双曲线的一条渐近线方程为,则双曲线的离心率为()ABCD4.5.在给定双曲线中,过焦点垂直于实轴的弦长为,焦点到对应准线的距离为,则该双曲线的离心率为()ABCD6.如图,和分别是双曲线()的两个焦点,和是觉得圆心,以为半径的圆与该双曲线左支的两个交点,且是等边三角形,则双曲线的离心率为()ABCD7.设、分别是椭圆()的左、右焦点,是其右准线上纵坐标为(为半焦距)的点,且,则椭圆的离心率是()ABCD8.设、分别是双曲线的左、右焦点,若双曲线上存在点,使,且,则双曲线离心率为()ABCD9.已知双曲线()的右焦点为,若过点且倾斜角为的直线与双曲线的右支有且只有一种交点,则此双曲线离心率的取值范畴是()ABCD10.椭圆()的焦点为、,两条准线与轴的交点分别为、,若,则该椭圆离心率的取值范畴是()A.B.C.D.答案:1.已知椭圆的长轴长是短轴长的2倍,∴,椭圆的离心率,选D。2.由可得故选D3.双曲线焦点在x轴,由渐近线方程可得,故选A4.5.不妨设双曲线方程为(a>0,b>0),则有,据此解得e=,选C6.解析:如图,和分别是双曲线的两个焦点,和是觉得圆心,觉得半径的圆与该双曲线左支的两个交点,且△是等边三角形,连接AF1,∠AF2F1=30°,|AF1|=c,|AF2|=c,∴,双曲线的离心率为,选D。7.由已知P(),因此化简得.8.设F1,F2分别是双曲线的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,设|AF2|=1,|AF1|=3,双曲线中,,∴离心率,选B。9.双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支有且只有一种交点,则该直线的斜率的绝对值不大于等于渐近线的斜...