高中数学必修4两角和与差的正弦、余弦、正切教学课件VIP免费

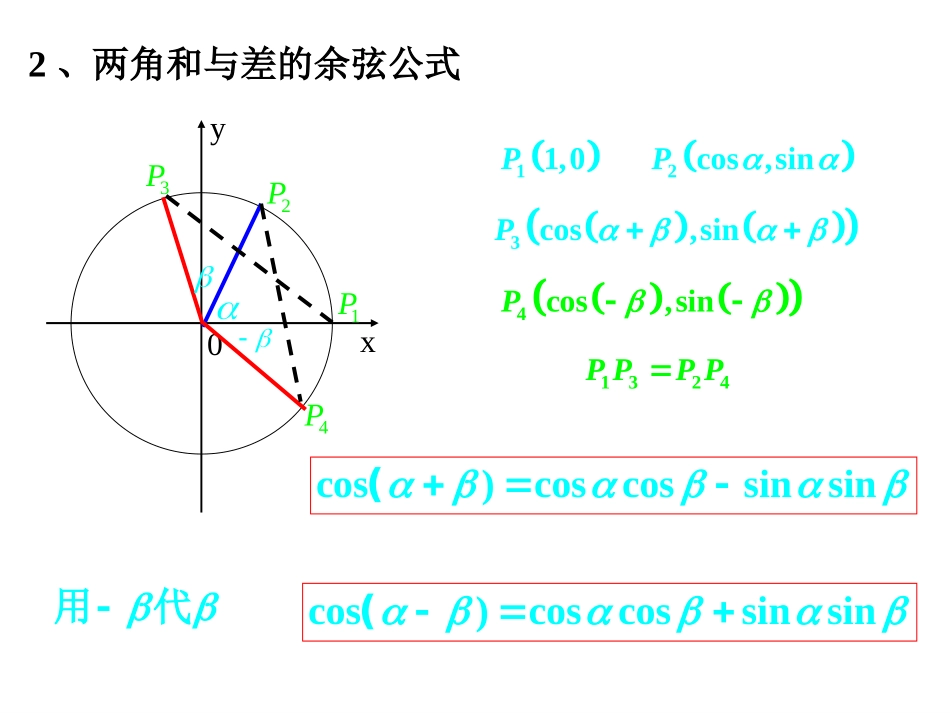
两角和与差的正弦、余弦、正切1、两点间的距离公式xy0Q1P1N1M2N2M111()Pxy，222()Pxy，11212PQMMxx21212PQNNyy221212221212PPPQPQxxyy2P2、两角和与差的余弦公式xy01P2P3P4P11,0P2cos,sinP3cos,sinP4cos,sinP1324PPPPcos)coscossinsin(cos)coscossinsin(用代3、两角和与差的正弦公式)](2cos[)sin(sin)2sin(cos)2cos(])2cos[(sincoscossinsin()sincoscossin用代sin()sincoscossin两角和与差的余弦公式、正弦公式cos)coscossinsin(cos)coscossinsin(sin()sincoscossinsin()sincoscossin)(C()C()S()S4、两角和与差的正切公式sincoscossintan()coscossinsin，得到以可以将分子、分母都除若coscos,0coscostantantan()1tantan()T用代tantantan()1tantan()T技巧小结:tanα+tanβtan(α+β)=1-tanαtanβtanα-tanβtan(α-β)=1+tanαtanβ常见变形：tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)tantan(1tanαtanβ)=tan()1.、不查表求cos105与cos15coscoscoscos45sin60sin4512322222264（1）105（6045）=60解：coscoscoscos45sin60sin451232222262.4（2）15（60-45）=603).2332、已知cos=，，2，求cos(5解：223cos2sin1cos1cos()coscossinsin3331322343.103=，，25345534553sincos,22cos).233、已知=，，，=-，34求(解：5sincos2337cos,sin24cos)coscossinsin57343527.122=，，33=-，4(32-43coscos()0,2cos.1474、已知=，=-，,1751求提示：coscos().拆角思想:7cos()cos(),2,43,cos2.4445、已知=，=-，且+55-求提示：cos2cos(.)()拆角思想:62sin3sin3,2cos3cos4cos().、已知求的值).cos()2()1(:22构造分析22(2sin3sin)(2cos3cos)251312(coscossinsin)25cos()1解：sinAsinABA2cosABAsin)()(左边sinAsinABA2cossinABAcoscosABAsin)()()(证明：sinAsinABAcoscosABAsin)()(sinAABAsin)(sinAsinB右边原式成立。练习：ooo203010分析：解：oooocos20sin20)20302cos（原式oooooocos20sin20)sin20sin30cos202(cos30oooocos20sin20)sin2021cos20232(3ooo2cos10sin208cos20、求的值。,sincoscossintantan分析：的值呢？及出能否由已知条件分别求sincoscossin解：将已知条件中的两个式子展开得32sincoscossin51sincoscossin307cossin3013sincos1371330307sincoscossintantan211tan,tan560,tan.xx、已知是方程的根求的值2:tan,tan3510tan().xx练习已知是方程的两根，求的值tantan,tantantantantan()1tantan求的值，而分析:对于是方程的两根,我们应想到韦达定理,tan,tan练习:1tan18tan423tan18tan422tan20tan30tan30tan40tan40tan201、求值2,:1tan1tan2.4ABCABAB在中求证31tan11tan21tan31tan431tan44.求的值