高中数学 第二章 正弦定理课件2 北师大版必修5 课件VIP免费

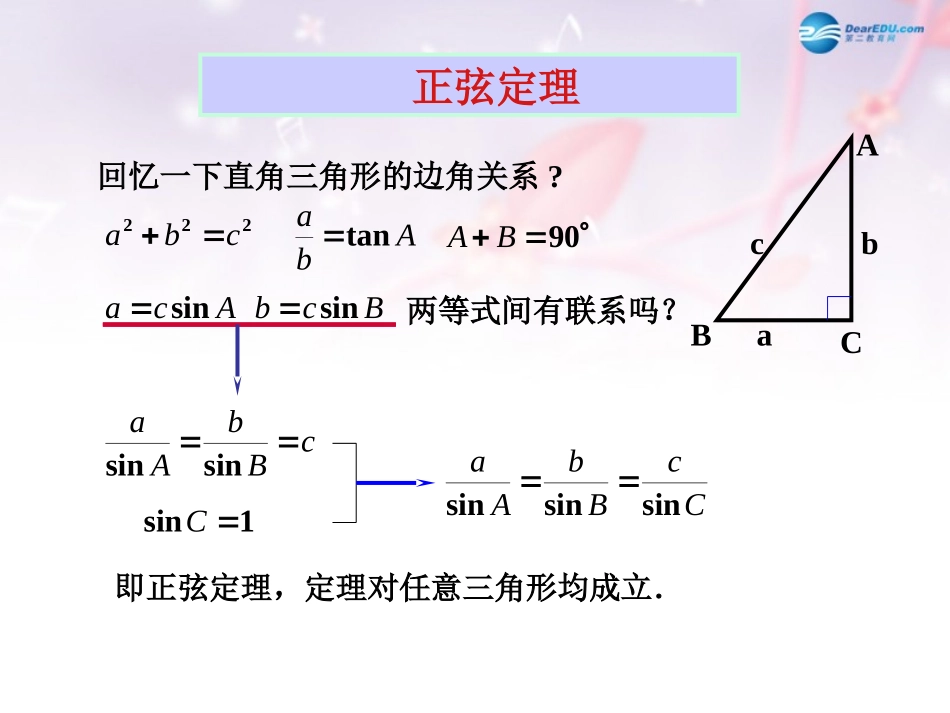
正弦定理正弦定理回忆一下直角三角形的边角关系?ABCcba222cbaAcasinBcbsinAbatan90BA两等式间有联系吗？cBbAasinsin1sinCCcBbAasinsinsin即正弦定理，定理对任意三角形均成立．正弦定理CcBbAasinsinsin正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即正弦定理可以解什么类型的三角形问题？已知两角和任意一边，可以求出其他两边和一角；已知两边和其中一边的对角，可以求出三角形的其他的边和角。一般地，把三角形的三个角A,B,C和它的对边a,b,c叫做三角形的元素已知三角形的几个元素求其他元素的过程叫做解三角形正弦定理例题讲解解三角形中，已知，在例,9.42,8.81,0.321cmaBAABC2.66)8.810.32(180)(180BAC定理，解：根据三角形内角和)(1.800.32sin8.81sin9.42sinsincmABab根据正弦定理，)(1.740.32sin2.66sin9.42sinsincmACac根据正弦定理，正弦定理例题讲解)11(,40,28,202cmAcmbcmaABC，边长精确到角度精确到解三角形。中，已知，在例.8999.02040sin28sinsinaAbB解：根据正弦定理，116,64,1800BBB或所以因为).(3040sin76sin20sinsin,76)6440(180)(18064)1(cmACacBACB时，当).(1340sin24sin20sinsin,24)11640(180)(180116)2(cmACacBACB时，当正弦定理例题讲解例3在中，，求的面积S．ABC)13(2,60,45aCBABCBacCabsin21sin21Abcsin21hABCaABCahS21三角形面积公式解：75)(180CBA∴由正弦定理得4426)22)(13(2sinsinABab326)23(4)13(221sin21CabSABC正弦定理中的比值常数典例1.在△ABC中，A，B，C所对的三边分别为a，b，c，若a=2bsinA，求B。（1）在中，一定成立的等式是（）ABCBbAaAsinsin.BbAaBcoscos.AbBaCsinsin.AbBaDcoscos.（2）若A,B,C是⊿ABC的三个内角，则sinA+sinB____sinC.)(sin3sin,2)3(等于则中，在BBBCABCA.b/aB.a/bC.a/cD.c/ac>B正弦定理练习：（1）在中，一定成立的等式是（）ABCBbAaAsinsin.BbAaBcoscos.AbBaCsinsin.AbBaDcoscos.CABC（2）在中，若，则是()A．等腰三角形B．等腰直角三角形C．直角三角形D．等边三有形2cos2cos2cosCcBbAaABCD正弦定理练习：（3）在任一中，求证：ABC0)sin(sin)sin(sin)sin(sinBAcACbCBa证明：由于正弦定理：令CkcBkBAkasin,sin,sin左边＝代入左边得：)sinsinsinsinsinsinBCACABCBCABAksinsinsinsinsin(sin∴等式成立=右边0在⊿ABC中，若acosA=bcosB,求证：⊿ABC是等腰三角形或直角三角形。利用正弦定理证明“角平分线定理”典例2已知a，b，c分别是△ABC中角A，B，C的对边，已知(a2+b2)sin(A-B)=(a2-b2)sin(A+B)(A≠B)，试判断△ABC的形状。典例3在△ABC中，有试判断此三角形的形状。典例4在△ABC中，求证：典例5在△ABC中，如果且B为锐角，试判断此三角形的形状。三角形面积计算公式典例1在△ABC中，a=3，b=5，cosC为方程10x2－29x－21=0的根，求△ABC的面积。典例2在△ABC中，若AB=2，BC=5，S△ABC=4，求的值。