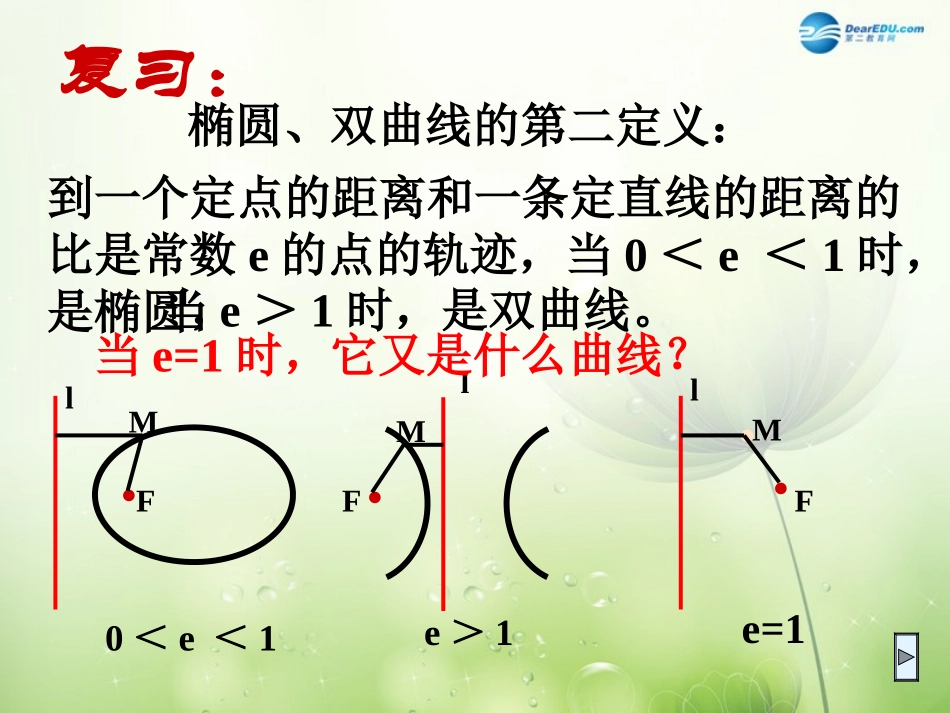
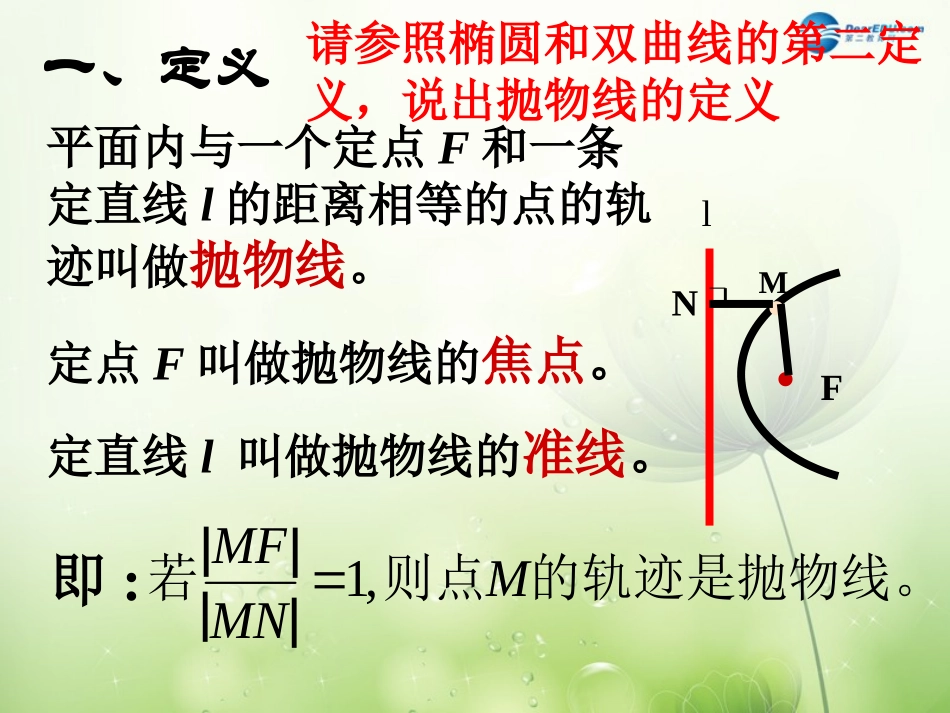
复习:椭圆、双曲线的第二定义:到一个定点的距离和一条定直线的距离的比是常数e的点的轨迹,当0<e<1时,是椭圆,·MFl0<e<1lF·Me>1·FMl·e=1当e>1时,是双曲线。当e=1时,它又是什么曲线?平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。定点F叫做抛物线的焦点。定直线l叫做抛物线的准线。一、定义的轨迹是抛物线。则点若MMNMF,1即:︳︳︳︳··FMlN请参照椭圆和双曲线的第二定义,说出抛物线的定义二、标准方程··FMlN如何建立直角坐标系?想一想yxoy=ax2+bx+cy=ax2+cy=ax2二、标准方程xyo··FMlNK︱KF︱=p则F(,0)l:x=-p2p2设点M的坐标为(x,y),由定义可知,化简得y2=2px(p>0)2)2(2pxypx2方程y2=2px(p>0)即为开口向右的抛物线的标准方程。其中p为正常数,它的几何意义是焦点到准线的距离yxo﹒﹒yxoyxo﹒yxo﹒图形焦点准线标准方程例1(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;变式:已知抛物线的方程是y=-6x2,求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程。练习:课本P132/4小结:1、椭圆、双曲线与抛物线的定义的联系及其区别;2、抛物线的四种标准方程,会运用抛物线的定义、标准方程求它的焦点、准线、方程;3、注重数形结合的思想。