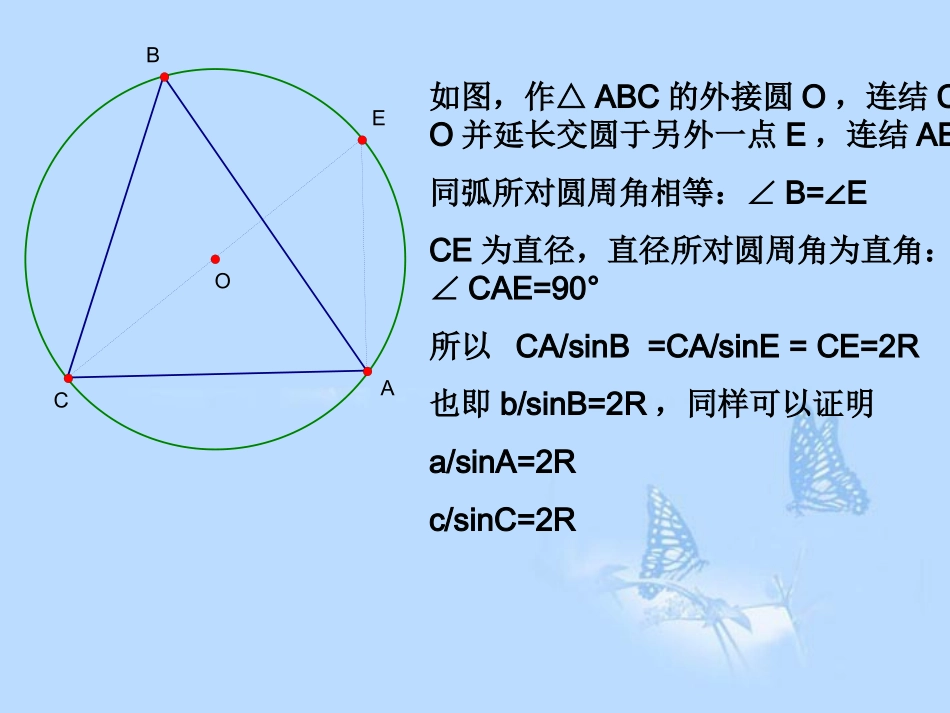
(第1课时)假如已知三角形三边长,则该三角形是唯一确定了,相应的几何量也应该可以用三边长表示。古代数学家经过漫长研究,逐渐找到众多几何量的等量关系。比如:设s=(a+b+c)/2____________△ABC的面积△=√s(s-a)(s-b)(s-c)(海伦公式)外接圆半径R=abc/(4)△内切圆半径r=2/(a+b+c)△A∠平分线的长度fA=2bcos(A/2)/(b+c)___________顶点A对应的中线的长度,ma=√(2b2+2c2-a2)/4sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)=s/RcosA+cosB+cosC=1+4sin(A/2)sin(B/2)sin(C/2)=1+r/R.....EOBCA如图,作△ABC的外接圆O,连结CO并延长交圆于另外一点E,连结AE。同弧所对圆周角相等:∠B=E∠CE为直径,直径所对圆周角为直角:∠CAE=90°所以CA/sinB=CA/sinE=CE=2R也即b/sinB=2R,同样可以证明a/sinA=2Rc/sinC=2R•通过对直角三角形边角关系的研究,发现正弦定理,然后给出一般证明。•理解正弦定理的推导过程,掌握正弦定理。•能简单应用正弦定理来求三角形的边或角。•重点:理解正弦定理的推导过程,掌握正弦定理。•难点:能简单应用正弦定理来求三角形的边或角。直角三角形中ABCcbasinsinabABcccBbAasinsin1sinCCcBbAasinsinsin即正弦定理,定理对任意三角形均成立.如何证明定理对任意三角形均成立?所以asinB=bsinA,得到.sinsinBbAa.sinsinCcBbABCcbaD当ABC是钝角三角形时,以上等式仍然成立吗?同理,在ABC中,例1:如图,当ABC是锐角三角形时,设边AB上的高是CD,根据三角函数的定义,CD=asinB,CD=bsinA,正弦定理在一个三角形中,各边和它所对角的正弦的比相等,即解三角形:一般地,把三角形的三个角A,B,C,及其对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形。CcBbAasinsinsin正弦定理可以解什么类型的三角形问题?(1)已知两角和任意一边,可以求出其他两边和一角;(2)已知两边和其中一边的对角,可以求出三角形的其他的边和角。sinsinsin2222sin2sin21.2.3.(sin3)abccabcABCabcRRRRARBRC56631:31:21:3:1102.2.3.4.C或或内容:合作探究案例1、变式1、例2、例3(时间:5分钟)要求:1、组长组织成员有序地、有重点地讨论。2、联系相关知识、明确思路、组织答案。3、探讨如何规范做题思路和规律方法的总结。4、组长分好工,选好代表准备展示,记录好本组内仍存在的疑问,准备质疑。点评要求:①所有同学充满激情、声音洪亮、踊跃展示。②上台点评的同学做好记录,做好判决准备。③上台点评的同学做判决时,先给予打分,并解释所给分数的合理性,同时针对问题要发表自己组的意见,其它同学记录要点,修改答案,以备辩论。展示点评例1:第1组第2组变式1:第3组第4组例2:第5组第6组例3:第7组第8组83163335262121.2.