高中数学必修第二册双曲线及其标准方程 课件VIP免费

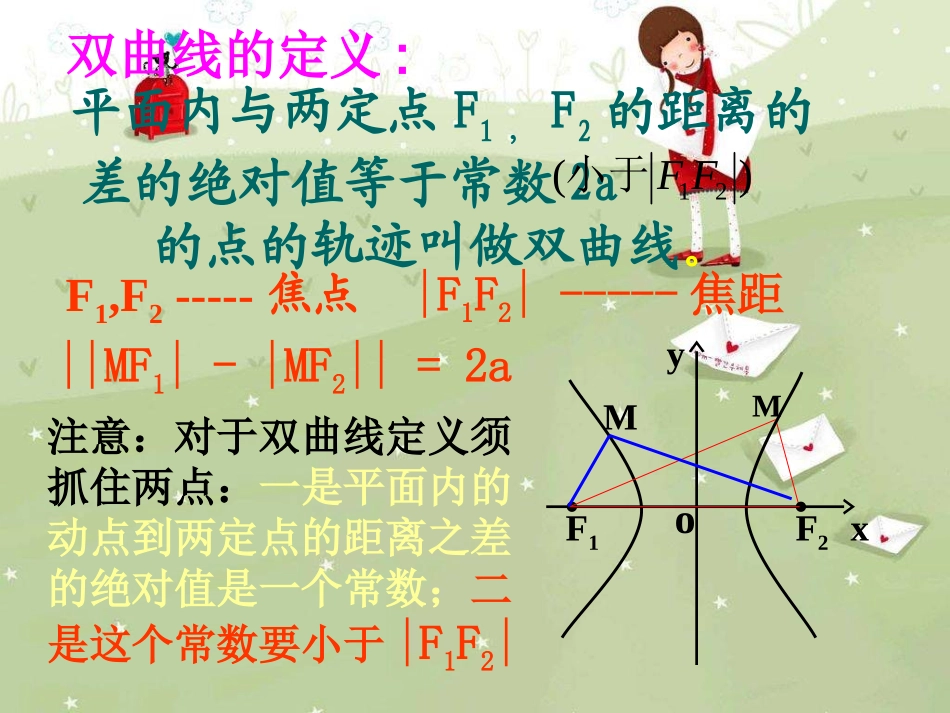
定义图象方程焦点a.b.c的关系yoxF1F2··yoF1F2··|MF1|+|MF2|=2a（2a>|F1F2|）a2=b2+c2F(±c,0)F(0,±c)oF1F2···)0(12222babyaxo双曲线的定义:平面内与两定点F1，F2的距离的差的绝对值等于常数2a的点的轨迹叫做双曲线。)(21FF小于F1,F2-----焦点||MF1|-|MF2||=2a|F1F2|-----焦距.F2.F1Myox注意：对于双曲线定义须抓住两点：一是平面内的动点到两定点的距离之差的绝对值是一个常数；二是这个常数要小于|F1F2|M请思考？1、平面内与两定点的距离的差等于常数2a（小于|F1F2|）的轨迹是什么？2、平面内与两定点的距离的差的绝对值等于常数（等于|F1F2|）的轨迹是什么？3、平面内与两定点的距离的差的绝对值等于常数（大于|F1F2|）的轨迹是什么？双曲线的一支是在直线F1F2上且以F1、F2为端点向外的两条射线不存在相关结论：1、当||MF1|-|MF2||=2a<|F1F2|时，2、当||MF1|-|MF2||=2a=|F1F2|时，3、当||MF1|-|MF2||=2a>|F1F2|时,M点的轨迹不存在4、当||MF1|-|MF2||=2a=0时，P点轨迹是双曲线其中当|MF1|-|MF2||=2a时，M点轨迹是与F2对应的双曲线的一支；当|MF2|-|MF1|=2a时，M点轨迹是与F1对应的双曲线的一支.M点轨迹是在直线F1F2上且以F1和F2为端点向外的两条射线。M点的轨迹是线段F1F2的垂直平分线。xyo设M（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)常数为2aF1F2M即(x+c)2+y2-(x-c)2+y2=+2a_以F1,F2所在的直线为X轴，线段F1F2的中点o为原点建立直角坐标系1.建系.2.设点．3.列式．|MF1|-|MF2|=2a如何求这优美的曲线的方程？4.化简.F1F2xOyaycxycx2)()(2222222222)(2)(ycxaycx222)(ycxaacx)()(22222222acayaxac222bac)0,0(12222babyax焦点在y轴上的双曲线的标准方程想一想F2F1yxoF1(0,-c),F2(0,c)222bac,焦点位置确定：椭圆看分母大小双曲线看x2、y2的系数正负焦点在y轴上的双曲线的图象是什么？标准方程怎样求？x2与y2的系数符号，决定焦点所在的坐标轴，当x2,y2哪个系数为正，焦点就在哪个轴上，双曲线的焦点所在位置与分母的大小无关。注：例1、已知双曲线的焦点为F1(-5,0),F2(5,0)双曲线上一点到焦点的距离差的绝对值等于6，则(1)a=_______,c=_______,b=_______(2)双曲线的标准方程为______________(3)双曲线上一点Ｐ，|PF1|=10,则|PF2|=_________3544或16||PF1|-|PF2||=6例2、已知双曲线两个焦点的坐标为F1(-5,0)、F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程。解：因为双曲线的焦点在x轴上，所以设它的∵2a=62c=10∴a=3c=5∴b2=52-32=16∴所求双曲线的标准方程为)00(12222babyax标准方程为11692222yx例3：k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是（)解：原方程化为：A、焦点在x轴上的椭圆C、焦点在y轴上的椭圆B、焦点在y轴上的双曲线D、焦点在x轴上的双曲线∵k>0∴k2+1>01+k>0∴方程的曲线为焦点在y轴上的双曲线。故选（B）111222kkyx课堂练习：1、已知点F1(-8,3)、F2(2,3)，动点P满足|PF1|-|PF2|=10，则P点的轨迹是()A、双曲线B、双曲线一支C、直线D、一条射线2、若椭圆与双曲线的焦点相同,则a=)0(14222ayax12322yx3D3、说明下列方程各表示什么曲线。4)3()3()1(2222yxyx5)3()3()2(2222yxyx6)3()3()3(2222yxyx方程表示的曲线是双曲线方程表示的曲线是双曲线的右支方程表示的曲线是x轴上分别以F1和F2为端点，指向x轴的负半轴和正半轴的两条射线。课堂小结：本节课学习了双曲线的定义、图象和标准方程，要注意使用类比的方法，仿照椭圆的定义、图象和标准方程的探究思路来处理双曲线的类似问题。作业：教材P108习题8.3第3题