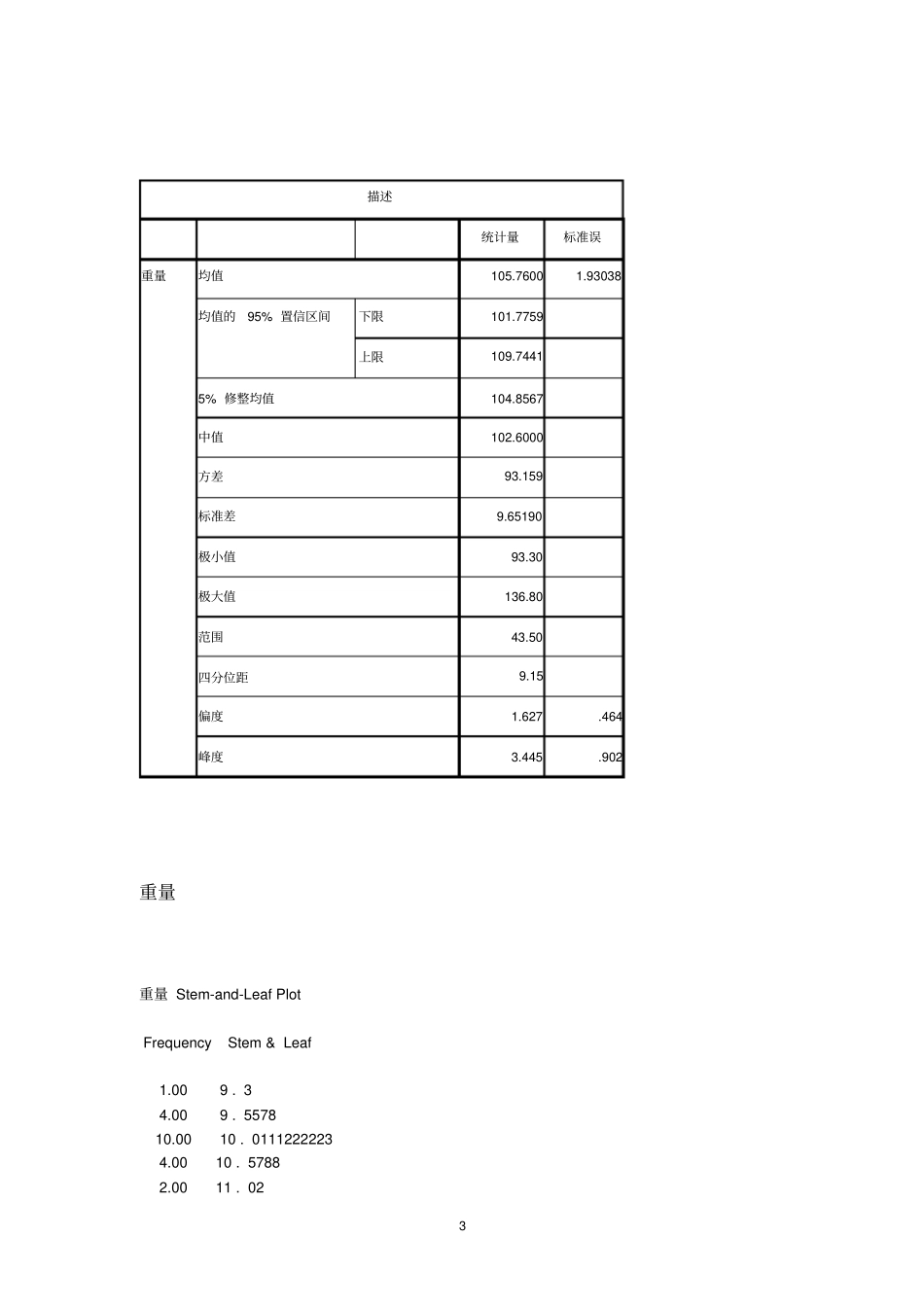
1例题7.5一家食品生产企业以生产袋装食品为主,每天的产量大约为8000袋左右。按规定每袋的重量应为100g。为对产品质量进行检测,企业质检部门经常要进行抽检,以分析每袋重量是否符合要求。现从某天生产的一批食品中随机抽取25袋,测得每袋重量如表7—2所示。表7—225袋食品的重量112.5101.0103.0102.0110.5102.6107.595.0108.8115.6100.0123.5102.0101.6102.2116.695.497.8108.6105.0136.8102.8101.598.493.3已知产品重量的分布,且总体标准差为10g,试估计该天产品平均质量的置信区间,以为95%建立该种食品重量方差的置信区间。解:已知δ=10,n=25,置信水平1-α=95%,Zx/2=1.962案例处理摘要案例有效缺失合计N百分比N百分比N百分比重量25100.0%0.0%25100.0%3描述统计量标准误重量均值105.76001.93038均值的95%置信区间下限101.7759上限109.74415%修整均值104.8567中值102.6000方差93.159标准差9.65190极小值93.30极大值136.80范围43.50四分位距9.15偏度1.627.464峰度3.445.902重量重量Stem-and-LeafPlotFrequencyStem&Leaf1.009.34.009.557810.0010.01112222234.0010.57882.0011.0242.0011.562.00Extremes(>=124)Stemwidth:10.00Eachleaf:1case(s)例7.6某地区教育管理部门香菇鸡两所中学的学生高考时的英语平均分之差,为此在两所中学独立抽取两个随机样本,有关数据如图所示中学1中学2n1=46n2=33x1=86x2=78s1=5.8s2=7.2例7.7为估计两种方法组装产品所需时间的差异,分别对两种不同的组装方法各随机安排12个工人,每个工人组装一件产品所需的时间列表如图。求平均时间差值的置信区间方法一方法二28.327.630.122.229.031.037.633.832.120.028.830.236.031.737.226.038.532.034.431.228.033.430.026.5解:已知,置信水平95%,方差相等,服从正态分布56例7.8仍沿用例7.7的数据,假定第一种方法随机安排12个工人,第二种方法随机安排8个工人,即n1=12,,n2=8,数据如下表。求产品所需平均时间差值的置信区间。方法一方法二28.327.6730.122.229.031.037.633.832.120.028.830.236.031.737.226.538.534.428.030.0解:已知,方差不等,置信区间水平95%897.9由10名学生组成一个随机样本,让他们分别采用A和B两套试卷进行测试,结果如表7—8所示。表7—810名学生两套试卷的得分学生编号试卷A试卷B差值d17871726344193726111489845591741764951-2768551387660161098577810553916假定两套试卷分数之差服从正态分布,试建立两套试卷平均分数之差的95%的置信区间。117.10在某个电视节目的收视率调查中,从农村随机调查了400人,有32%的人收看了该节目;从城市随机调查了500人。有45%的人收看了该节目,试以95%的置信水平估计城市与农村收视率差别的置信区间。解:设城市收视率P1=45%,农村收视率P2=32%。当a=0.05时,Za/2=1.96。因此,置信区间为:单样本T检验:12比较均值—单样本T检验按右侧的“选项”137.11.为研究男女学生在生活费支出(单位:元)上的差异,在某大学各抽取名男学生和女学生,得到下面的结果:男学生:均值520方差:260女学生:均值480方差:280试以90%的置信水平估计男女学生生活费支出方差比的置信区间。分析—配对样本T检验14这里没有原始数据,所以无法在变量1和变量2区域中输入数据区域,就无法做下去了。而且不像SPSS的区间估计和假设检验一个菜单可以做出,Excel的假设检验就真只有假设检验,不会顺便做区间估计的。15167.12拥有工商管理学士学位的大学毕业生年薪的标准差大约为2000元,假定想要估计年薪95%的置信区间,希望估计误差为400元,应抽取多大样本量?7.13根据以往的生产统计,某种产品的合格率约为90%,现要求估计误差为5%,在求95%的置信区间时,应抽取多少个样本作为产品?