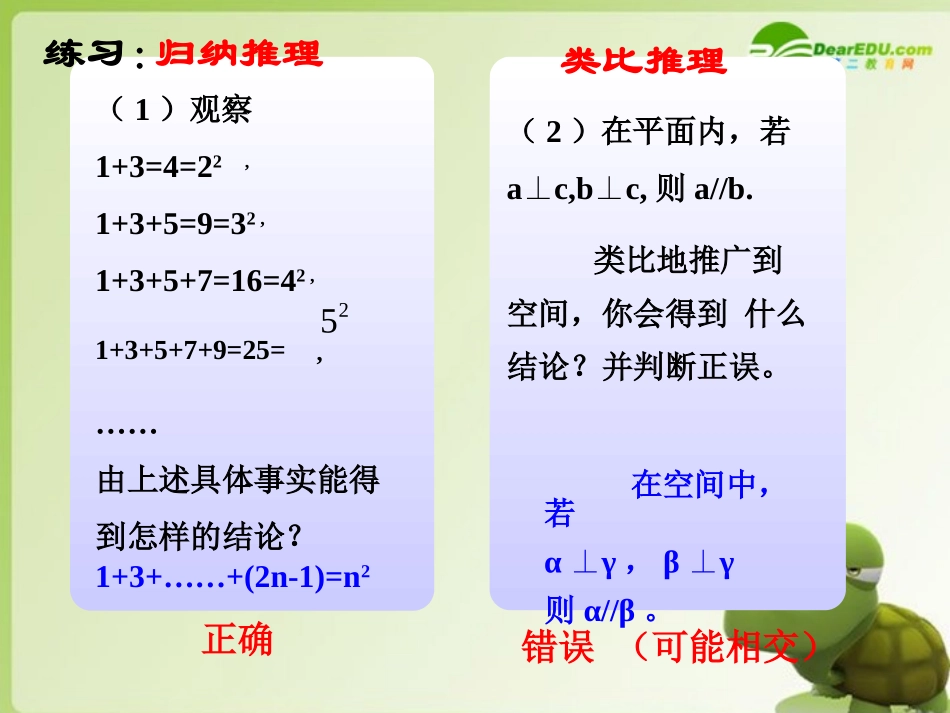
(1)观察1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=,……由上述具体事实能得到怎样的结论?(2)在平面内,若ac,bc,⊥⊥则a//b.类比地推广到空间,你会得到什么结论?并判断正误。正确错误(可能相交)1+3+……+(2n-1)=n2在空间中,若αγ⊥,βγ⊥则α//β。25练习:归纳推理类比推理归纳推理和类比推理的共同点归纳推理和类比推理的共同点归纳推理归纳推理和类比推理类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合合情推理情推理.从具体问题出发观察、分析、比较、联想归纳、类比提出猜想合情推理合情推理通俗地说,合情推理是指“合乎情理”的推理。观察与思考1.所有的金属都能导电,2.一切奇数都不能被2整除,3.三角函数都是周期函数,4.全等的三角形面积相等所以铜能够导电.因为铜是金属,所以(2100+1)不能被2整除.因为(2100+1)是奇数,所以是tan周期函数因为tan三角函数,那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1全等,2.1.2演绎推理从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎(逻辑)推理.演绎推理是由一般到特殊的推理.⑴大前提--已知的一般原理;⑵小前提--所研究的特殊情况;⑶结论----根据一般原理,对特殊情况做出的判断.一、演绎推理的定义:二、演绎推理的一般模式:“三段论”观察与思考1.所有的金属都能导电,2.一切奇数都不能被2整除,3.三角函数都是周期函数,4.全等的三角形面积相等所以铜能够导电.因为铜是金属,所以(2100+1)不能被2整除.因为(2100+1)是奇数,所以是tan周期函数因为tan三角函数,那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1全等,大前提小前提结论大前提:M是P小前提:S是M结论:S是P若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P.三、三段论推理的依据MS1.全等三角形面积相等那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1相似,2.相似三角形面积相等那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1相似,想一想???错因:大前提是错误的,所以结论是错误的。错因:推理形式错误,结论是错误的。例1:用三段论的形式写出下列演绎推理。(1)三角形内角和180°,等边三角形内角和是180°233.0(1)分析:省略了小前提:“等边三角形是三角形”。(2)是有理数。(2)分析:省略了大前提:“所有的循环小数都是有理数。”解:所有的三角形内角和都是180°,所以等边三角形内角和是180°。等边三角形是三角形,233.0小前提:“是循环小数。”例2:证明函数f(x)=-x2+2x在(-∞,1]上是增函数.满足对于任意x1,x2∈D,若x10因为x1