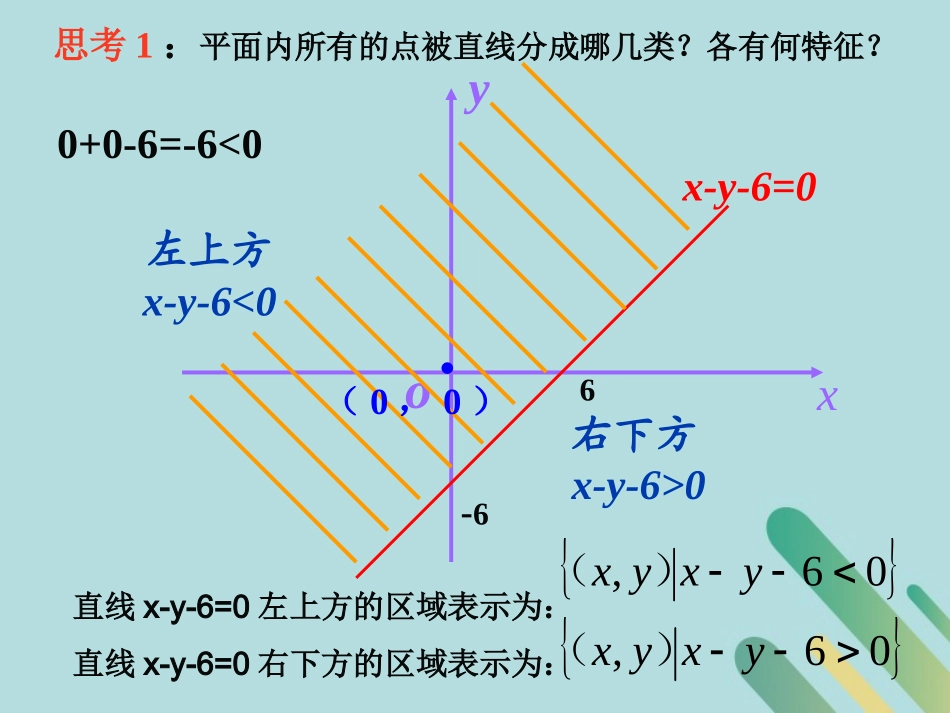
3.4.1二元一次不等式(组)与平面区域在平面直角坐标系中,点的集合{(x,y)|x-y=6}表示什么图形?导直线0+0-6=-6<0xyo6-6右下方x-y-6>0x-y-6=0(0,0)左上方x-y-6<0思考1:平面内所有的点被直线分成哪几类?各有何特征?直线x-y-6=0左上方的区域表示为:直线x-y-6=0右下方的区域表示为:06,yxyx)(06,yxyx)(在平面直角坐标系中,二元一次不等式Ax+By+C>0(<0)表示直线Ax+By+C=0某一侧所有点组成的平面区域。思考2:画出不等式2x+y-6<0表示的平面区域。xyo362x+y-6<02x+y-6=0平面区域的确定常采用“直线定界,特殊点定域”的方法。解:将直线2X+y-6=0画成虚线将(0,0)代入2X+y-6得0+0-6=-6<0原点所在一侧为2x+y-6<0表示平面区域(1)画直线Ax+By+C=0(2)在此直线的某一侧取一个特殊点(x0,y0),从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域。一般在C≠0时,取原点作为特殊点.1、点判别法:画不等式AX+BY+C>0表示的平面区域的方法2、结论法:同则上,异则下。说明:不等式AX+BY+C>0中B的符号与不等式符号相同时,则平面区域在直线上方;相反时,则平面区域在直线下方。二元一次不等式表示平面区域探究一例1画出下列不等式表示的平面区域:(1)2x+3y-6>0(2)4x-3y≤12OXY32OYX3-4应该注意的几个问题:1、若不等式中不含0,则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、理解“直线定界、特殊点定域”方法和结论法。否则应画成实线。二元一次不等式组表示平面区域二元一次不等式组表示平面区域探究二例2画出不等式组表示的平面区域3005xyxyxOXYx+y=0x=3x-y+5=0-55解:0-0+5>01+0>0例2画出不等式组表示的平面区域3005xyxyxOXYx+y=0x=3x-y+5=0-55解:0-0+5>01+0>0注:不等式组表示的平面区域是各不等式所表示平面区域的公共部分.不等式组表示平面区域的应用探究三则用不等式可表示为:020420yyxyx解:此平面区域在x-y=0的右下方,x-y≥0它又在x+2y-4=0的左下方,x+2y-4≤0它还在y+2=0的上方,y+2≥0Yox4-2x-y=0y+2=0x+2y-4=02检测1:求由三直线x-y=0;x+2y-4=0及y+2=0所围成的平面区域所表示的不等式.检A.(-∞,5)B.[7,+∞)C.[5,7)D.(-∞,5)∪[7,+∞)跟踪训练3(1)若不等式组x-y+5≥0,y≥a,0≤x≤2表示的平面区域是一个三角形,则实数a的取值范围是()检测2:解析如图,当直线y=a介于直线y=5(含该直线)与直线y=7(不含该直线)之间时,符合题意.所以5≤a<7,选C.检答案C