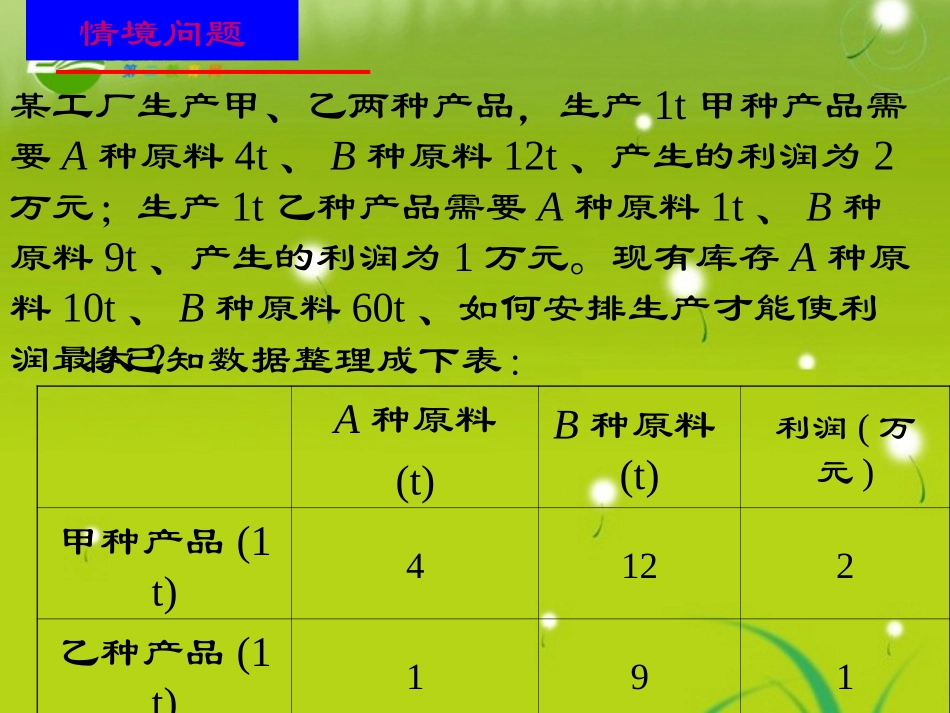
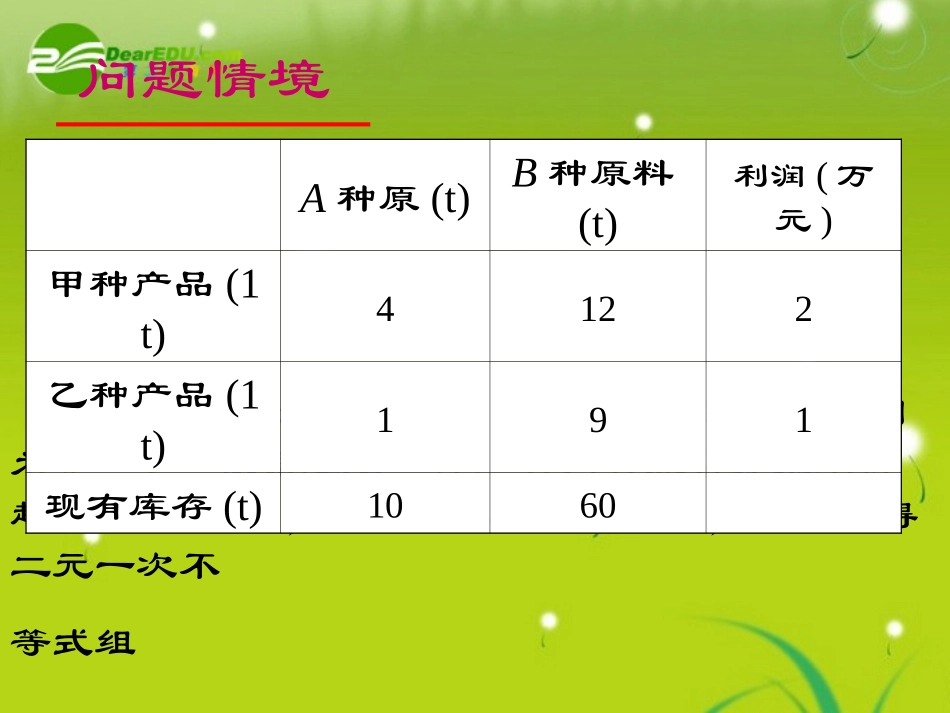
3.3.1二元一次不等式表示平面区域情境问题某工厂生产甲、乙两种产品,生产1t甲种产品需要A种原料4t、B种原料12t、产生的利润为2万元;生产1t乙种产品需要A种原料1t、B种原料9t、产生的利润为1万元。现有库存A种原料10t、B种原料60t、如何安排生产才能使利润最大?将已知数据整理成下表:A种原料(t)B种原料(t)利润(万元)甲种产品(1t)4122乙种产品(1t)191现有库存(t)1060问题情境设计划生产甲、乙两种产品的吨数分别为x,y,根据题意,A、B两种原料分别不得超过10t和60t,又产量不可能是负数,于是可得二元一次不等式组A种原(t)B种原料(t)利润(万元)甲种产品(1t)4122乙种产品(1t)191现有库存(t)1060即4x+y≤1012x+9y≤60x≥0y≥04x+y≤104x+3y≤20x≥0y≥0上述问题可以转化为如下的数学问题:在约束条件4x+y≤104x+3y≤20x≥0y≥0下,求出x,y,使利润P=2x+y(万元)达到最大如何解决这个问题?合作探究为了解决上面的问题我们可以分两个步骤:第一步研究问题中的约束条件,确定数对(x,y)的范围;第二步在第一步得的数对(x,y)的范围中,找出使达到最大的数对(x,y)。先讨论第一步。如图,直线l:4x+y=10将平面分成上、下两个平面区域,直线l上的点的坐标满足方程4x+y=10,即y=10-4x,直线l上方的平面区域中的点坐标满足不等式y>10-4x,直线l下方的平面区域中的点的坐标满足不等式y<10-4x.。xyol:4x+y=10yl:4x+y=10o104yx(y>10-4x)(y<10-4x.)xy=kx+b一般地,直线y=kx+b把平面分成两个区域如图0xy上半平面y>kx+b下半平面ykx+b表示直线上方的平面区域y>kx+b表示直线上方的平面区域〔总结与反思〕想一想?如何确定二元一次不等式Ax+By+C>0表示的平面区域?数学运用例1画出下列不等式表示的平面区域12)1(xy022yx)(解(1),(2)两个不等式所表示的平面区域如图所示12xyy=-2x+1yx01102yx0yx2202yx画出下列不等式表示的平面区域:(1)2x+3y-6>0(2)4x-3y≤12OXY32OYX3-4(1)(2)练习例2将下列各图中的平面区域(阴影部分)用不等式表示图(1)不包含y轴0yx(1)yx0(2)yx0(3)(1)x>0(2)6x+5y≤22(3)y>x解二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。确定步骤:直线定界,特殊点定域;若C≠0,则直线定界,原点定域;小结:应该注意的几个问题:1、若不等式中不含0,则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。否则应画成实线。