高中数学 104(二元一次不等式(组)表示平面区域)课件 湘教版必修4 课件VIP免费

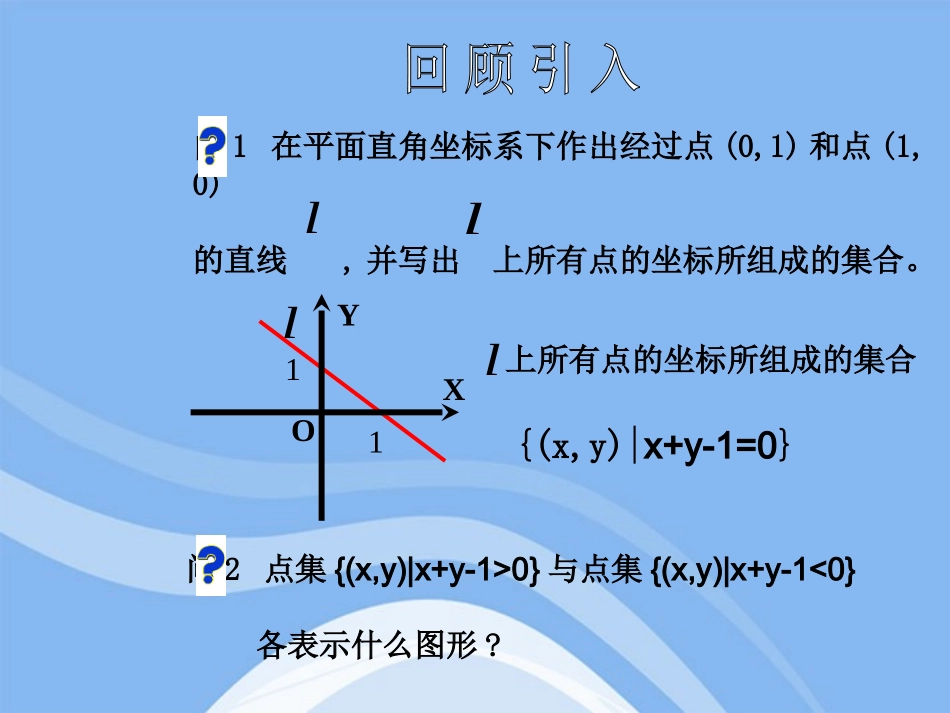
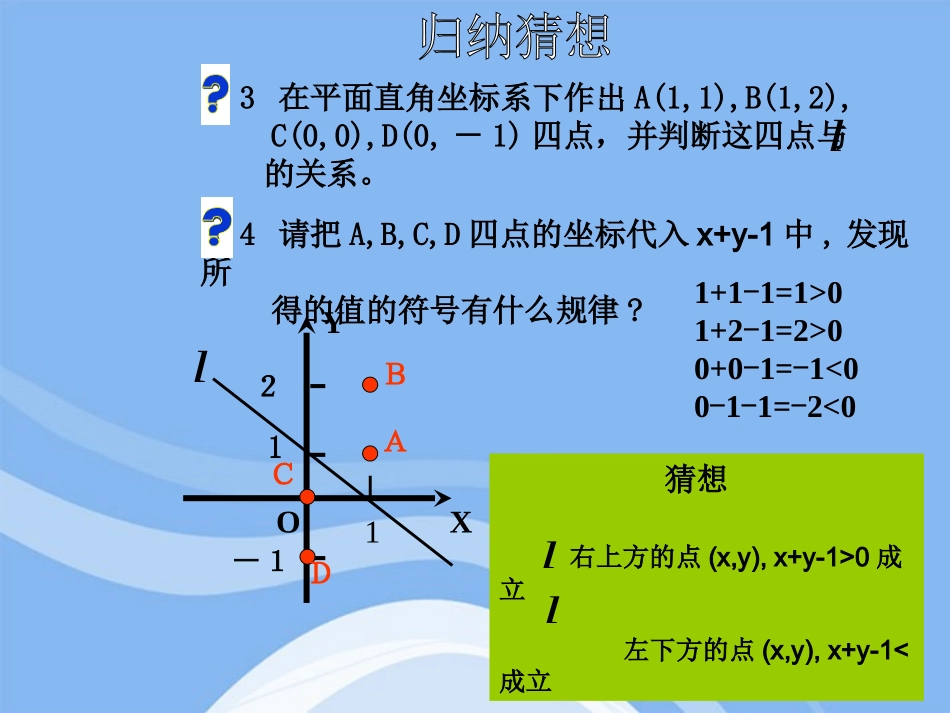
二元一次不等式表示平面区域OYX11l上所有点的坐标所组成的集合l{(x,y)|x+y-1=0}问1在平面直角坐标系下作出经过点(0,1)和点(1,0)的直线,并写出上所有点的坐标所组成的集合。ll问2点集{(x,y)|x+y-1>0}与点集{(x,y)|x+y-1<0}各表示什么图形?lOYX11２－１lＡＢＣＤ1+1-1=1>01+2-1=2>00+0-1=-1<00-1-1=-2<0猜想右上方的点(x,y),x+y-1>0成立左下方的点(x,y),x+y-1<成立ll问3在平面直角坐标系下作出A(1,1),B(1,2),C(0,0),D(0,－1)四点，并判断这四点与的关系。问4请把A,B,C,D四点的坐标代入x+y-1中,发现所得的值的符号有什么规律?M证明:如图,设M(x,y)为右上方区域内任一点lP过M作MP平行于x轴交于点P),(00yxl则00,yyxxOYX11lx+y-1=000yxyx1100yxyx由于M的任意性,故对于直线x+y-1=0右上方区域内任意点(x,y),都有x+y-1>0同理:对于直线x+y-1=0左下方区域内的任意一点(x,y),都有x+y-1<0x+y-1<0x+y-1>0OYX11l点集{(x,y)|x+y-1>0}表示直线x+y-1=0右上方平面区域点集{(x,y)|x+y-1<0}表示直线x+y-1=0左下方平面区域问2点集{(x,y)|x+y-1>0}与点集{(x,y)|x+y-1<0}各表示什么图形?（1）Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。（3）注意所求区域是否包括边界线。（2）在确定区域时，在直线的某一侧取一个特殊点，从的正负可以判断出Ax+By+C>0表示哪一侧的区域。一般在C≠0时，取原点作为特殊点。),(00yxCByAx00例1：画出不等式2x+y-6<0表示的平面区域。例2：画出不等式表示的平面区域。062yx2x+y-6<02×0+0–6<0虚线（不含边界）2x+y-6<02x+y-6=03xyo6)0,0(,06取原点c2x+y-6=0实线（含边界）取点（0，0）3xyo6062yx062yx06-002直线定界,特殊点定域若C≠0，则直线定界,原点定域特殊点(0,0)特殊点(0,0)或(0,1)或(0,-1)画出下列不等式表示的平面区域：(1)x-y+1<0;(2)x+y>0；(3)2x+5y-10≥0;x-y+1<0xyo1-1x-y+1=0（1）x-y+1<0取(0,0)0-0+1>0x+y>0x+y=0（2）x+y>0直线过（0，0）取（0，1）0+1>0xyo1xyo522x+5y-10≥02x+5y-10=0（3）2x+5y-10≥0取(0,0)0100502例2.画出不等式组表示的平面区域3005xyxyxOXYx+y=0x=3x-y+5=0注：不等式组表示的平面区域是各不等式所表示的平面区域的公共部分。画出下列不等式组表示的平面区域：9362323xyyxxyx(2)答案答案242,yyxxy(1)xyo24-2y=xx+2y=4y=-2242,yyxxyxyo12313x=32y=x3x+2y=63y=x+99362323xyyxxyx应该注意的几个问题：1、若不等式中不含0，则边界应画成虚线，否则应画成实线。2、画图时应非常准确，否则将得不到正确结果。3、熟记“直线定边界、特殊点定区域”方法的内涵。教材106页习题4学而时习之2题