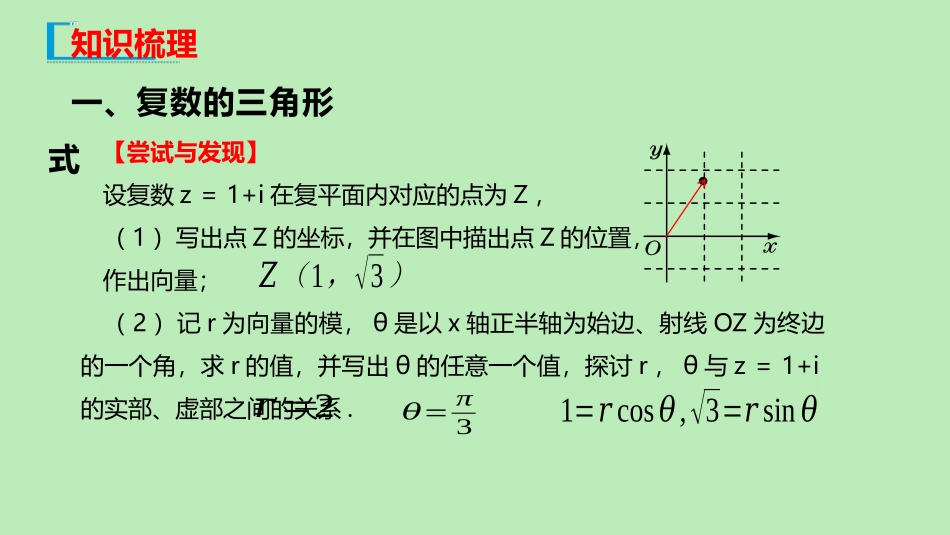
10.3复数的三角形式及其运算第十章复数学习目标1.通过复数的几何意义,了解复数的三角表示.2.了解复数的代数表示与三角表示之间的关系.3.了解辐角、辐角主值等概念.4.了解复数乘除运算的三角表示及其几何意义.重点:复数的三角表示.难点:复数乘除运算的三角表示及其几何意义.知识梳理一、复数的三角形式【尝试与发现】设复数z=1+i在复平面内对应的点为Z,(1)写出点Z的坐标,并在图中描出点Z的位置,作出向量;(2)记r为向量的模,θ是以x轴正半轴为始边、射线OZ为终边的一个角,求r的值,并写出θ的任意一个值,探讨r,θ与z=1+i的实部、虚部之间的关系.𝑍(1,√3)𝑟=2𝜃=π31=𝑟cos𝜃,√3=𝑟sin𝜃复数的三角形式的定义:一般地,如果非零复数z=a+bi(a,b∈)在复平面内对应点Z(a,b),且r为向量的模,θ是以x轴正半轴为始边、射线OZ为终边的一个角,则r=|z|=,根据任意角余弦、正弦的定义可知cosθ=,sinθ=.因此a=rcosθ,b=rsinθ,如图所示,从而z=a+bi=(rcosθ)+(rsinθ)i=r(cosθ+isinθ),上式的右边称为非零复数z=a+bi的三角形式(对应地,a+bi称为复数的代数形式),其中的θ称为z的辐角.显然,任何一个非零复数z的辐角都有无穷多个,而且任意两个辐角之间都相差2π的整数倍.特别地,在[0,2π)内的辐角称为z的辐角主值,记作argz.【名师点拨】为了求出一个非零复数的三角形式,只要求出这个复数的模,然后再找出复数的一个辐角(比如辐角主值)即可.例如,对于复数z=1+i来说,因为|z|=221(3)=2,cosθ=12,sinθ=32,所以可取θ=argz=3,从而z=1+i的三角形式为z=2cosisin33.这也可以通过如下方式得到.z=1+i=222222131(3)i1(3)1(3)=13222i=2cosisin33.因为0=0(cosθ+isinθ),其中θ可以为任意值,所以我们也称上式为复数0的三角形式.这样一来,任意复数都可以写成三角形式了.【特别提示】(1)复数的三角形式与代数形式一样,也是表示复数的一种方法,它们可以相互转化.(2)复数的代数形式是唯一的,但三角形式不唯一.(3)任何一个不为零的复数的辐角有无限多个值,但辐角主值只有一个;复数0的辐角是任意的,不讨论它的辐角主值.二、复数三角形式的乘除法1.复数三角形式的乘法法则【尝试与发现】设z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),试求出z1z2.提示:z1z2=r1(cosθ1+isinθ1)×r2(cosθ2+isinθ2)=r1r2[(cosθ1cosθ2-sinθ1sinθ2)+i(sinθ1cosθ2+cosθ1sinθ2)]=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].由此,我们可得到复数三角形式的乘法法则:r1(cosθ1+isinθ1)×r2(cosθ2+isinθ2)=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].z1的模乘以z2的模等于z1z2的模(简记:模相乘)z1的辐角与z2的辐角之和是z1z2的辐角(简记:辐角相加)例如,266cosisin×22cosisin=26262cosisin=222cosisin33.2.复数三角形式乘法的几何意义设z1,z2对应的向量分别为,,将绕原点旋转θ2,再将的模变为原来的r2倍,如果所得向量为,则对应的复数即为z1z2,如图所示.当θ2>0时,按逆时针方向旋转角θ2,当θ2<0时,按顺时针方向旋转角.又因为+i=i,所以一个复数与i相乘,从向量的角度来说,就相当于把这个复数对应的向量绕原点沿逆时针方向旋转,如图所示.上述两个复数三角形式的乘法及其几何意义,可以推广到有限个复数的三角形式相乘.特别地,如果n∈,则[r(cosθ+isinθ)]n=rn[cos(nθ)+isin(nθ)].3.复数三角形式的除法法则【尝试与发现】如果非零复数z的三角形式为z=r(cosθ+isinθ),利用两个共轭复数在复平面内对应的点关于x轴对称,写出的三角形式,并求出z的值.提示:一般地,如果非零复数z=r(cosθ+isinθ),那么-θ是的一个辐角,因此=r[cos(-θ)+isin(-θ)],而且z=r(cosθ+isinθ)×r[cos(-θ)+isin(-θ)]=r2[cos(θ-θ)+isin(θ-θ)...