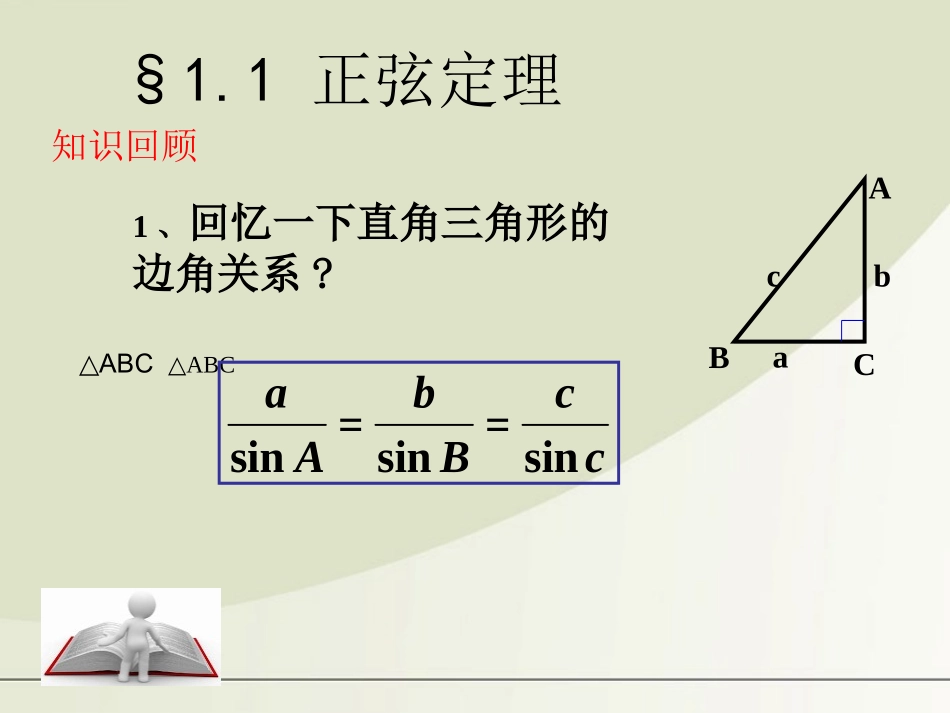
§1.1正弦定理知识回顾△ABCABC△ccBbAasin=sin=sin1、回忆一下直角三角形的边角关系?ABCcba•1、已知两角和任意一边,可以求出其他两边和一角。ccBbAasin=sin=sin•2、已知两边和其中一边的对角,可以求出三角形的其他的边和角。例题讲解例1在中,已知,求b(保留两个有效数字).ABC30,45,10CAcccBbAasin=sin=sin解:∵且CcBbsinsin105)(180CAB1930sin105sin10sinsinCBcb例2、在△ABC中,已知20=ab=28A=40求B(精确到1)和c(保留两个有效数字)8999.0=2040sin28=sin=sin0aAbB解:.116=,64=0201BB∴.76=)40+64(180=)+(180=,64=000010101ABCB时当.3040sin76sin20=sinsin=0011≈∴ACac.24=)40+116(180=)+(180=,116=000020202ABCB时当.1340sin24sin20=sinsin=0022≈∴ACacACB1abB2DccBbAasin=sin=sin在例2中,将已知条件改为以下几种情况,判断有几组解?60°ABCb(3)b=20,A=60°,a=15.(1)b=20,A=60°,a=;320(2)b=20,A=60°,a=;310变式拓展:ccBbAasin=sin=sin(3)b=20,A=60°,a=15.60°20AC(1)b=20,A=60°,a=;32060°20√3A20BC(2)b=20,A=60°,a=;310BC60°A20一解一解无解ccBbAasin=sin=sin练习1ccBbAasin=sin=sin()xxxf22log+=