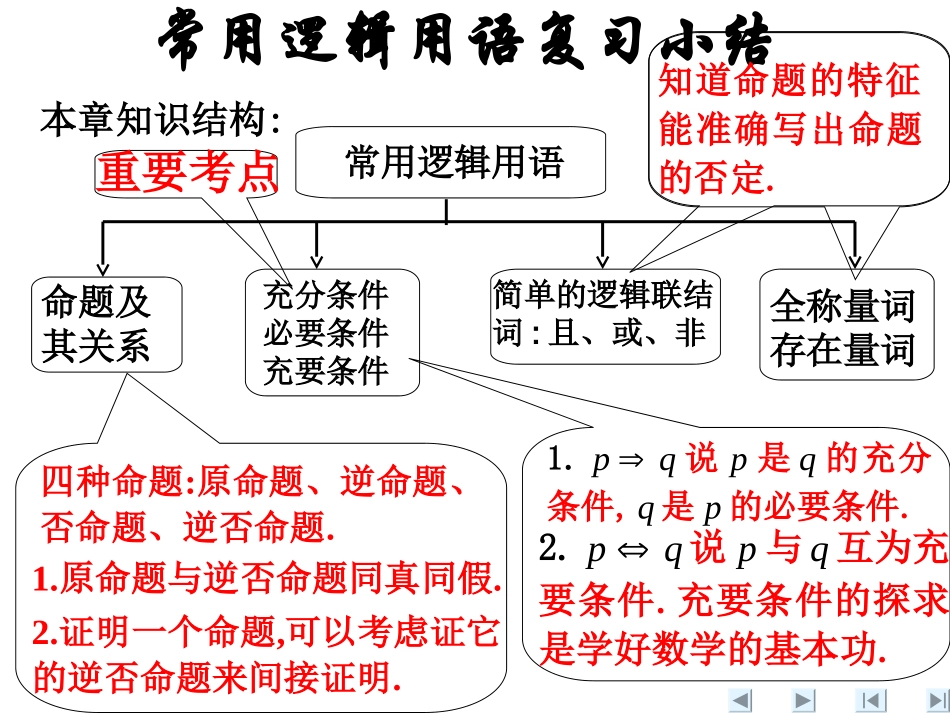
高中数学选修2—1第一章常用逻辑用语之知识整合与学段复习(2课时)常用逻辑用语知识是进行数学推理和思维必不可少的基本知识.通过本章的学习,使我们体会到逻辑用语的严谨性、准确性及其中蕴含的一些思维规律,甚至有些同学会认为我们好像是在“咬文嚼字”,而且有些思维是形式化的在进行,其实这种训练可以有助于我们正确理解数学概念、合理论证数学结论、准确表达数学内容.常用逻辑用语复习小结常用逻辑用语知识的学习,我们要充分品味逻辑用语的严谨性、准确性和其中蕴含的思维规律,但又不要刻意追求那些形式化又无实际意义的东西的推敲,贵在思维的熏陶。常用逻辑用语复习小结本章知识结构:常用逻辑用语命题及其关系全称量词存在量词充分条件必要条件充要条件简单的逻辑联结词:且、或、非四种命题:原命题、逆命题、否命题、逆否命题.1.原命题与逆否命题同真同假.2.证明一个命题,可以考虑证它的逆否命题来间接证明.1.pq说p是q的充分条件,q是p的必要条件.2.pq说p与q互为充要条件.充要条件的探求是学好数学的基本功.知道命题的特征.能准确写出命题的否定.重要考点四种命题形式及其关系注:(1)“互为”的;(2)原命题与其逆否命题同真同假.(3)逆命题与否命题同真同假.原命题若p,则q逆否命题若q,则p否命题若p,则q逆命题若q,则p互逆互否互否互逆互为逆否同真同假【例2】将命题“a>0时,函数y=ax+b的值随x值的增加而增加”改写成“若p则q”的形式,并写出否命题.【解法一】原命题改为:a>0时,若x增加,则函数y=ax+b的值随之增加.否命题为:a>0时,若x不增加,则函数y=ax+b的值也不增加.【解法二】原命题也可改为:当x增加时,若a>0,则函数y=ax+b的值随之增加.否命题为:当x增加时,若a≤0,则函数y=ax+b的值不增加.【例1】下列语句:①是无限循环小数;②x2-3x+2=0;③当x=4时,2x>0;④垂直于同一条直线的两条直线必平行吗?⑤一个数不是合数就是质数;⑥难道菱形的对角线不互相平分吗?⑦把门关上.其中不是命题的是.2②④⑦【例3】有A、B、C三个盒子,其中一个内放有一个苹果,在三个盒子上各有一张纸条A盒子上的纸条写的是:“苹果在此盒内”B盒子上的纸条写的是:“苹果不在此盒内”C盒子上的纸条写的是:“苹果不在A盒内”如果三张纸条中只有一张写的是真的,请问苹果究竟在哪个盒子里?【分析】就苹果在A、B、C逐一检验三个盒子上的纸条的真假.【解】若苹果在A盒内,则A、B两个盒子上的纸条写的为真,不合题意.若苹果在B盒内,则A、B两个盒子上的纸条写的是假,C盒子上的纸条写的为真,符合题意,即苹果在B盒内.同样,若苹果在C盒内,则B、C两盒子上的纸条写的为真,不合题意.综上,苹果在B盒内.【例4】对于命题“正方形的四个内角相等”,下面判断正确的是()A.所给命题为假B.它的逆否命题为真C.它的逆命题为真D.它的否命题为真【解析】先写出“正方形的四个内角相等”的逆命题、否命题、逆否命题,然后逐一判断.【答案】B【例5】写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假:(1)若a,b都是偶数,则a+b是偶数;(2)若m>0,则方程x2+x-m=0有实根.练习一:1.有下列四个命题:①“||3x若,则33xx或”的逆命题;②命题“a、b都是偶数,则a+b是偶数”的逆否命题是“a+b不是偶数,则a、b都不是偶数”;③若有命题p:7≥7,q:ln2>0,则p且q是真命题;④若一个命题的否命题为真,则它的逆命题一定是真.其中真命题为()(A)①④(B)②③(C)②④(D)③④2.命题:“若220xx,则x≠–1且x≠2”的否命题是_______.3.已知Ryx,,且2yx,求证:yx,中至少有一个大于1.D若220xx,则1x或2x.3.已知Ryx,,且2yx,求证:yx,中至少有一个大于1.法二:假设yx,均不大于1,即11,xy≤且≤2xy则≤,这与已知条件2yx矛盾yx,中至少有一个大于1法一:假设yx,均不大于1,即11,xy≤且≤2xy则≤,这说明原命题的逆否命题成立∴原命题成立.练习与巩固3.已知命题p:关于x的方程x2+mx+1=0有两个不等的负实根;命题q:关于x的方程4x2+4(m-2)x+1=0无实根,已知命题p和q中,一个为真命题,一个为假命题,...