高三数学数列的极限 课件VIP免费

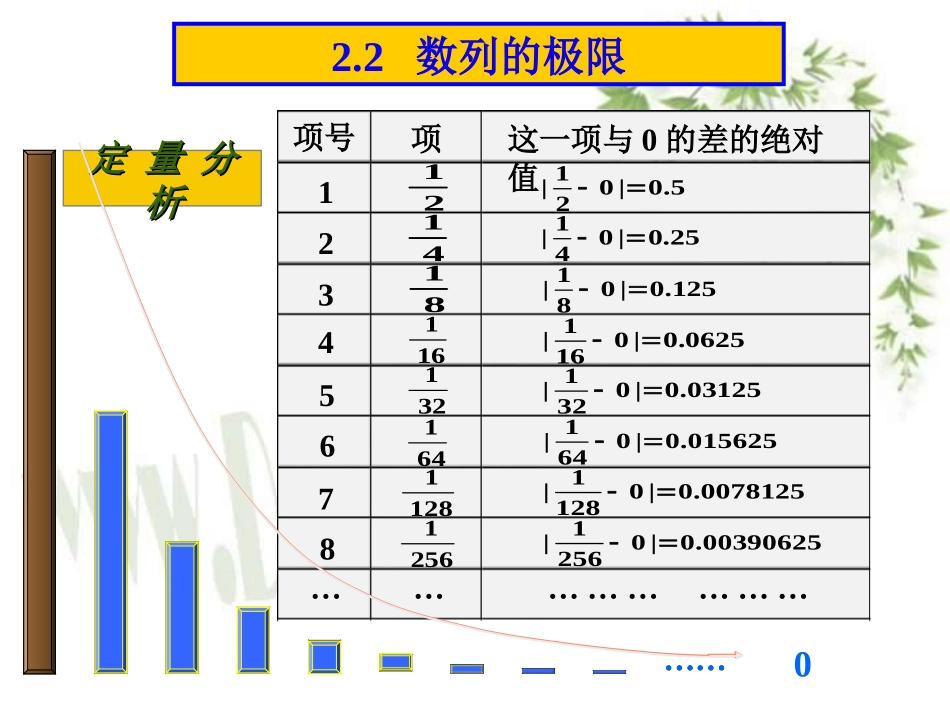
极限概念极限概念与与数列的极限数列的极限战国时代哲学家庄周著的《庄子战国时代哲学家庄周著的《庄子··天下篇》引用过一句话：天下篇》引用过一句话：一尺之棰日取其半万世不竭一尺之棰日取其半万世不竭..……2.2数列的极限定量分定量分析析项号项这一项与0的差的绝对值12345678………214181161321641128125615.0|021|25.0|041|125.0|081|0625.0|0161|03125.0|0321|015625.0|0641|0078125.0|01281|00390625.0|02561|………………………02.2数列的极限三国时的刘徽提出的““割圆求周割圆求周””的方法.他把圆周分成三等分、六等分、十二等分、二十四等分、···这样继续分割下去,所得多边形的周长就无限接近于圆的周长.割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣.2.2数列的极限12345678…项号边数内接多边形周长定量分定量分析析圆的半径21R2412632.5980762113533.0000000000003.1058285412303.132628613281483.139350203047963.1410319508911923.1414524722853843.141557607912……………2.2数列的极限2.2数列的极限0-13121，，，，n1013101310132（1），，，，，1433221nn（2），，，，２，nn)1(3111（3）分析当n无限增大时，下列数列的项的变化趋势及共同特征:na..............共同特性：不论这些变化趋势如何，随着项数n的无限增大，数列的项无限地趋近于常数ana3递减无限趋近1递增无限趋近0无限趋近摆动n趋向于无穷大aannlim数列极限的描述性定义na一般地，如果当项数无限增大时，无穷数列的项无限地趋近于某个常数，(即无限地接近0),nnaaaan那么就说数列以为极限，或者说naaana是数列的极限na（1）是无穷数列n（2）无限增大时，不是一般地趋近于，而是naa“无限”地趋近于a（3）数值变化趋势：递减的、递增的、摆动的读作“当n趋向于无穷大时，的极限等于a”na或“limit当n趋向于无穷大时等于a”na注意:2.2数列的极限例题讲解例1、考察下面的数列，写出它们的极限：（1）；，，，，，31271811n（2）；，，，，，n1057995.695.65.6；,)2(1,,81,41,21n（3）解：（1）数列的项随n的增大而减小，但大于0，且当n无限增大时，无限地趋近于0，因此，数列的极限是0．31n31n31n70aannnalim数列是否存在极限若存在极限99.0nna100)(n1nan2nanna)1(14nnanaannlim存在不存在存在存在不存在41n000－20数列的极限是唯一的有穷数列没有极限099.0n)(lim为常数CCCnaannnalim数列是否存在极限若存在极限aannlimnan1nannann3)1(nna)31(59999.0nna如果，那么1||annalim0存在存在存在存在不存在5000na“无限”地趋近于一个常数an)31(n31n19999.0n0000)(lim)2(是常数CCnnn1lim)1(0C,)3(时当1a0limnan1x221344356已知数列已知数列2,,,,,,,6556433421,n11+（-1)n+1(1)写出这个数列的各项与1的差的绝对值;(2)第几项后面的所有项与1的差的绝对值都小于0.1?都小于0.001?都小于0.0003?(3)1是不是这个数列的极限?解：解：（（11））这个数列的各项与1的差的绝对值依次是1，.,n1,,31,21..10101nn解得令)(nnn111111（（22））..100000101nn解得令..313333000301nn解得令（（33））是这个数列的极限1.例3.1、数列极限的直观描述性定义），无限地接近（即，无限地趋近于某个常数的项无穷数列无限增大时，一般地，如果当项数0aaaaannnn的极限是数列或者说为极限，以那么就说数列nnaaaaaannlim2、利用定义求数列极限3、常用数列的极限)(lim)2(是常数CCnnn1lim)1(0C,)3(时当1a0limnan