高中数学 322函数模型及其应用(一)课件 新人教A版必修1 课件VIP免费

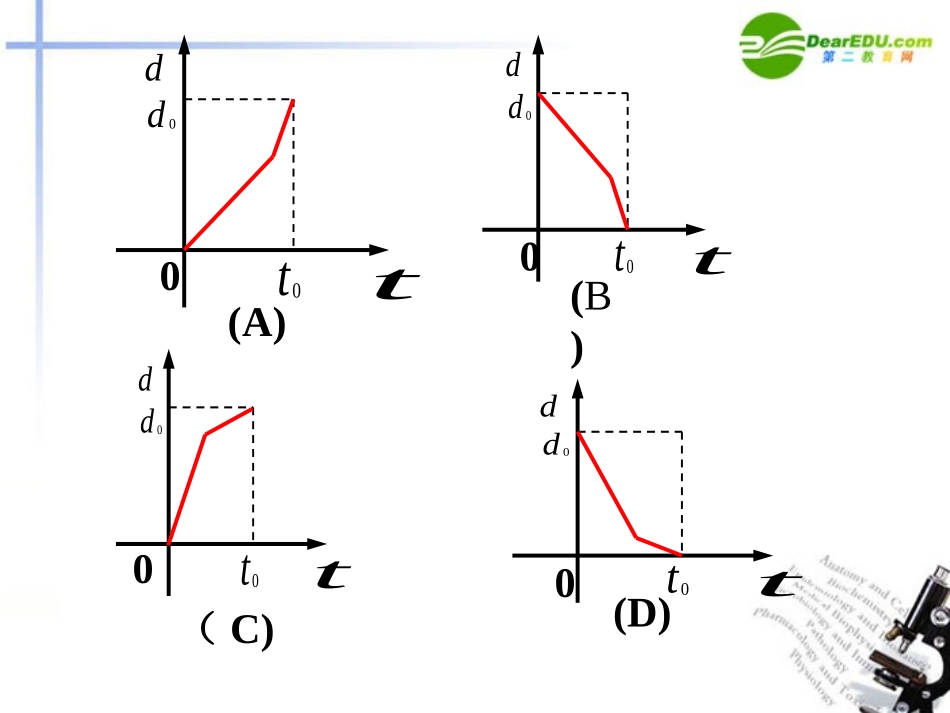
3.2.2函数模型及其应用问题某学生早上起床太晚，为避免迟到，不得不跑步到教室，但由于平时不注意锻炼身体，结果跑了一段就累了，不得不走完余下的路程。如果用纵轴表示该生到教室的距离，横轴表示出发后的时间，则下列四个图象比较符合实际的是（）tt0d0d0(A)tt0d0d0(B)tt0d0d0(D)tt0d0d0（C)908070605040302010vt12345例1一辆汽车在某段路程中的行驶速度与时间的关系如图所示：（1）求图中阴影部分的面积，并说明所求面积的实际含义；（2）假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km，试建立汽车行驶这段路程时汽车里程表读数skm与时间th的函数解析式，并作出相应的图象解：（1）阴影部分的面积为阴影部分的面积表示汽车在这5小时内行驶的为360km。501801901751651360这个函数的图象如图2所示。ts例2人口增长模型:其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率.年份1950195119521953195419551956195719581959人数/万人55196563005748258796602666145662828645636599467207下表是1950年~1959年我国的人口数据资料:,0rteyy(2)如果按表上表的增长趋势,大约在哪一年我国的人口达到13亿?(1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;.0200.01951,56300)1(55196,,,,1959~1951)1(:11921rrrrr年的人口增长率可得由年的人口增长率分别为设解.0184.0,0222.0,0276.0,0223.0,0197.0,0250.0,0229.0,0210.098765432rrrrrrrr，同理可得0221.09)(921rrrr于是,1951~1959年期间,我国人口的年平均增长率为.,551961959~1951,551960221.00Nteyyt增长模型为年期间的人口则我国在令5000055000600006500070000012345ty6789).()(55196,0221.0下图的图象并作出函数点图根据上表的数据作出散Nteyt由上图可以看出,所得模型与1950~1959年的实际人口数据基本吻合.小结本节内容主要是运用所学的函数知识去解决实际问题，学会掌握函数应用的基本方法和步骤．求函数)1(log221xy的单调递增区间。