高中数学 2.3.4平面向量共线的坐标表示课件 新人教A版必修4 课件VIP免费

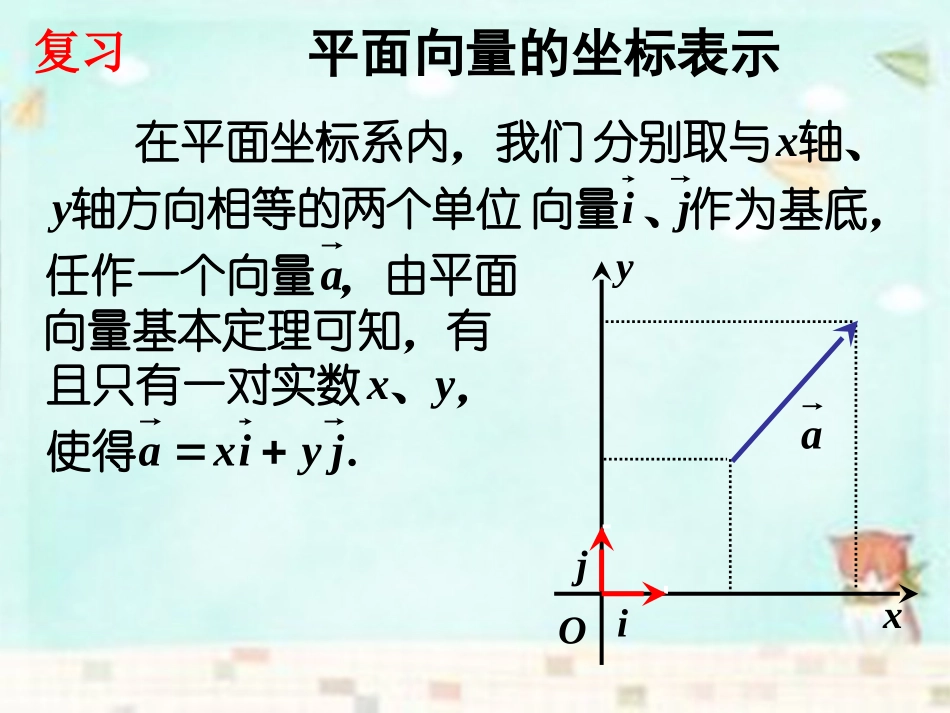
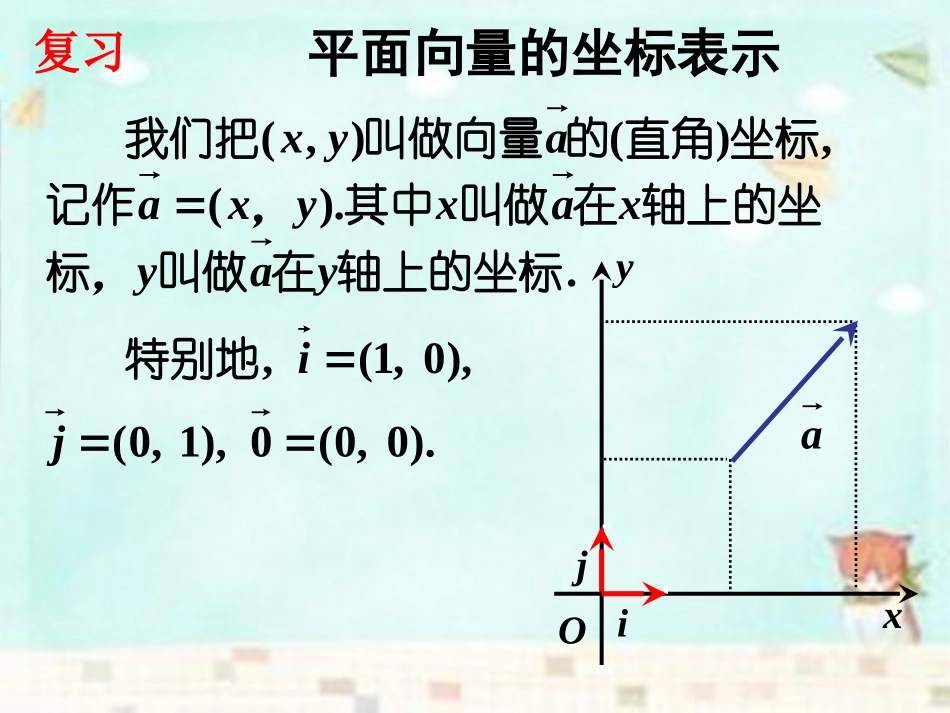
2.3.4平面向量共线的坐标表示平面向量的坐标表示.jyixayxajiyx使得，、且只有一对实数向量基本定理可知，有，由平面任作一个向量作为基底，、向量轴方向相等的两个单位轴、分别取与在平面坐标系内，我们xOijay复习.).(,)(),(轴上的坐标在叫做标，轴上的坐在叫做其中，记作坐标直角的叫做向量我们把yayxaxyxaayx平面向量的坐标表示xOijay,)0,1(,i特别地.)0,0(0,)1,0(j复习平面向量的坐标运算),()()(21212121yxayyxxbayyxxba，，两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.复习平面向量的坐标运算).,(),,(),,(12122211yyxxAByxByxA则若一个向量的坐标等于表示此向量的有向线段的终点坐标减去始点的坐标.复习两个向量共线的充要条件是什么?那么，如何用坐标表示两个共线向量?..0,,,,2211bababyxbyxa，使当且仅当存在实数共线，与其中设复习.0)0(1221时当且仅当共线与yxyxbba推导过程：,2121yyxx),(),(2211yxyxba得：由.01221yxyx：消去.0),,(),,(2211byxbyxa其中设向量共线的坐标表示:)0(//bbaba.01221yxyx向量共线的两个等价条件或)0(//bbaba.01221yxyx向量共线的两个等价条件或?.22211xyxy能不能写成讲解范例.,//),,6(),2,4(ybayba求且已知.1例0264,6,2,4,//yybaba解：3y例2.已知A(1,1)，B(1,3)，C(2,5)，试判断A，B，C三点之间的位置关系.讲解范例三点共线.,)2,(),1(xxbxa求共线且方向相同与若向量例3.讲解范例例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxyxyOP1P2P(1)1212121()2(,)22OPOPOPxxyy�解：（1）所以，点P的坐标为1212(,)22xxyyxyOP1P2P(2)xyOP1P2P例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxy解：（2）xyOP1P2P(2)xyOP1P2P例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxy解：（2）21131PPOP12131OPOPOP213132OPOP32,322121yyxx解：（2）那么若,2121PPPPPPOPOP11xyOP1P2P例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxy解：（2）那么若,2121PPPPxyOP1P2P例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxyyyxxyyxx2211,21,另、yyyyxxxx21212121有32,322121yyxxP点坐标解有xyOP1P2P例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxy解：（2）32,322212121yyxxPPPPP，同理可得，若例4.设点P是线段P1P2上的一点，P1、P2的坐标分别是（1）当点P是线段P1P2的中点时，求点P的坐标；（2）当点P是线段P1P2的一个三等分点时，求点P的坐标。1122(,),(,)xyxy思考.若P1P:PP2＝如何求点P的坐标?xyOP1P2P)0(//bbaba.01221yxyx向量共线的两个等价条件课堂小结