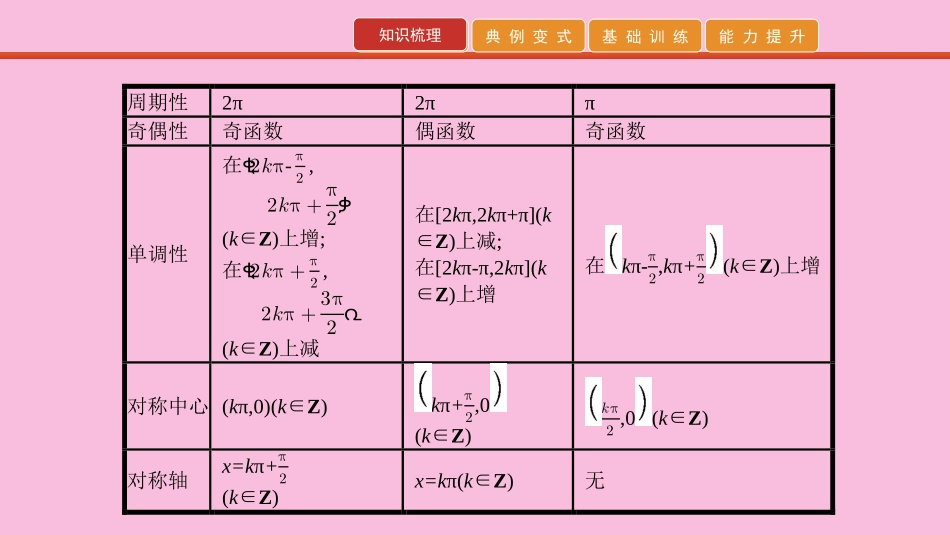
知识梳理典例变式基础训练能力提升第10讲三角函数的图象与性质知识梳理典例变式基础训练能力提升知识梳理1.基本三角函数的图象与性质三角函数正弦函数y=sinx余弦函数y=cosx正切函数y=tanx图象定义域RRx∈R,且x≠kπ+π2,k∈Z值域[-1,1][-1,1]R知识梳理典例变式基础训练能力提升知识梳理周期性2π2ππ奇偶性奇函数偶函数奇函数单调性在ቂ2𝑘π-π2,2𝑘π+π2ቃ(k∈Z)上增;在ቂ2𝑘π+π2,2𝑘π+3π2൨(k∈Z)上减在[2kπ,2kπ+π](k∈Z)上减;在[2kπ-π,2kπ](k∈Z)上增在kπ-π2,kπ+π2(k∈Z)上增对称中心(kπ,0)(k∈Z)kπ+π2,0(k∈Z)𝑘π2,0(k∈Z)对称轴x=kπ+π2(k∈Z)x=kπ(k∈Z)无知识梳理典例变式基础训练能力提升知识梳理2.y=Asin(ωx+φ)的有关概念y=Asin(ωx+φ)(A>0,ω>0)振幅周期频率相位初相AT=2𝜋ωf=1T=ω2𝜋ωx+φφ知识梳理典例变式基础训练能力提升知识梳理3.用五点法画y=Asin(ωx+φ)一个周期内的简图用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示:x-φω-φω+𝜋2ω𝜋-φω3𝜋2ω−φω2𝜋-φωωx+φ0𝜋2π3𝜋22πy=Asin(ωx+φ)0A0-A0知识梳理典例变式基础训练能力提升知识梳理4.三角函数图象变换的两种方法(ω>0)知识梳理典例变式基础训练能力提升知识梳理5.三角函数的奇偶性与对称性(1)y=Asin(ωx+φ),当φ=kπ(k∈Z)时为奇函数;当φ=kπ+π2(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ+π2(k∈Z)求得,对称中心的横坐标可由ωx+φ=kπ,(k∈Z)解得.(2)y=Acos(ωx+φ),当φ=kπ+π2(k∈Z)时为奇函数;当φ=kπ(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ(k∈Z)求得,对称中心的横坐标可由ωx+φ=kπ+π2(k∈Z)解得.y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数;对称中心的横坐标可由ωx+φ=𝑘π2(k∈Z)解得,无对称轴.知识梳理典例变式基础训练能力提升典例变式题型一三角函数的定义域、值域.【例1】(1)函数y=ඥ2sin𝑥-ξ3的定义域为()A.ቂπ3,2π3ቃB.ቂ2𝑘π+π3,2𝑘π+2π3ቃ(k∈Z)C.ቀ2𝑘π+π3,2𝑘π+2π3ቁ(k∈Z)D.ቂk𝜋+𝜋3,k𝜋+2𝜋3ቃ(k∈Z)(2)(2019·长沙模拟)函数f(x)=cos2x+6cosቀπ2-𝑥ቁ的最大值为()A.4B.5C.6D.7知识梳理典例变式基础训练能力提升典例变式【解析】(1)由2sinx-ξ3≥0得sinx≥ξ32,∴π3+2kπ≤x≤23π+2kπ(k∈Z),故选B.(2) f(x)=cos2x+6cosቀπ2-𝑥ቁ=cos2x+6sinx=1-2sin2x+6sinx=-2ቀsin𝑥-32ቁ2+112,又sinx∈[-1,1],∴当sinx=1时,f(x)取得最大值5.故选B.【答案】(1)B(2)B知识梳理典例变式基础训练能力提升典例变式【规律方法】(1)三角函数定义域的求法:求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.(2)三角函数值域的不同求法①利用sinx和cosx的值域直接求.②把所给的三角函数式变换成y=Asin(ωx+φ)的形式求值域.③把sinx或cosx看作一个整体,转换成二次函数求值域.④利用sinx±cosx和sinxcosx的关系转换成二次函数求值域.知识梳理典例变式基础训练能力提升典例变式变式训练一1.函数y=1tan𝑥-ξ3的定义域为.ቄ𝑥≠𝑘π+π2且𝑥≠𝑘π+π3,𝑘∈Zቅ【解析】由已知得ቊ𝑥≠𝑘π+π2,𝑘∈Ztan𝑥≠ξ3∴൝𝑥≠𝑘π+π2,𝑘∈Z𝑥≠𝑘π+π3,𝑘∈Z∴所求函数定义域为{x|x≠kπ+π2且x≠kπ+π3,k∈Z}.知识梳理典例变式基础训练能力提升典例变式2.求函数y=cos2x+sinxቀ|𝑥|≤π4ቁ的最大值与最小值.12−ξ22【解析】函数变为y=1-sin2x+sinx.设t=sinx,ቀ|𝑥|≤π4ቁ,∴t∈-ξ22,ξ22൨.函数变为f(t)=-t2+t+1=-ቀ𝑡-12ቁ2+54∴当t=12,即sinx=12,x=π6时,ymax=54.∴当t=-ξ22,即x=-π4时,ymin=12−ξ22.知识梳理典例变式基础训练能力提升典例变式3.函数y=sinx+cosx+sinxcosx的值域为.ቈ-1,12+ξ2【解析】设t=sinx+cosx,则sinxcosx=𝑡2-12(-ξ2≤t≤ξ2),y=t+12t2-12=12(t+1)2-1,当t=ξ2时,y取最大值为ξ2+12,当t=-1时,y取最小值为-1.所以函数值域为ቂ-1,12+ξ2ቃ.知识梳理典例变式基础训练能力提升典例变式题型二三角函数的单调性【例2】(1)函数f(x)=sinቀ-2𝑥+π3ቁ的单调减区间为.(2)已知ω>0,函数f(x)=sinቀ𝜔𝑥+π4ቁ的一个单调递减区间为ቂπ8,5π8ቃ,则ω=.(3)...