高中数学复习课件：离散型随机变量取值的均值二) 课件VIP免费

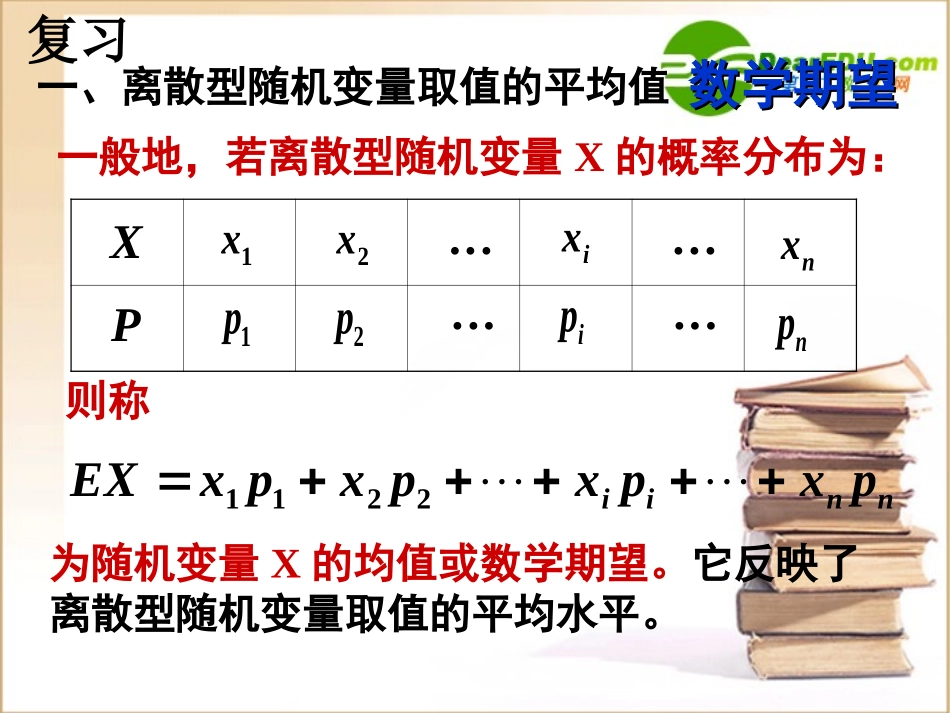
离散型随机变量取值的均值（二）一、离散型随机变量取值的平均值数学期望数学期望一般地，若离散型随机变量X的概率分布为：nniipxpxpxpxEX2211则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。P1xix2x······1p2pip······nxnpX复习二.求离散型随机变量取值的平均值的一般步骤•1.求随机变量X的概率分布列•2.代入nniipxpxpxpxEX2211三、基础训练三、基础训练1、随机变量ξ的分布列是ξ135P0.50.30.2(1)则Eξ=.2、随机变量ξ的分布列是2.4ξ47910P0.3ab0.2Eξ=7.5,则a=b=.0.40.1问题引入：例1.篮球运动员在比赛中每次罚球命中得1分，罚不中得0分．已知某运动员罚球命中的概率为0.7，他连续罚球3次；（1）求他得到的分数X的分布列；（2）求X的期望。离散型随机变量取值的均值（二）二项分布与超几何分布的均值例1.篮球运动员在比赛中每次罚球命中得1分，罚不中得0分．已知某运动员罚球命中的概率为0.7，他连续罚球3次；（1）求他得到的分数X的分布列；（2）求X的期望。X0123P33.0解：(1)X～B（3，0.7）2133.07.0C3.07.0223C37.0(2)322321337.033.07.023.07.013.00CCEX1.2EX7.03一般地，如果随机变量X服从二项分布，即X～B（n,p），则npEX猜想：证明：n),0,1,2,(kqpCk)P(ξknkkn0nnnknkkn1n11nn00nqpnCqpkCqpC1qpC0Eξ)qpCqpCqpCqpnp(C01n1n1n1)(k1)(n1k1k1n2n111n1n001n所以若ξ～B(n，p)，则Eξ＝np．证明：若ξ～B(n，p)，则Eξ＝np1().nnppqnp一般地，如果随机变量X服从二项分布，即X～B（n,p），则npEX小结：基础训练：一个袋子里装有大小相同的3个红球和2个黄球，从中有放回地取5次，则取到红球次数的数学期望是.3•例2.在10件产品中,有3件一等品,4件二等品,3件三等品.从这10件产品中任取3件,•求：取出的3件产品中一等品件数X的分布列和数学期望•（Ⅰ）解：由于从10件产品中任取3件的结果为，从10件产品中任取3件，其中恰有k件一等品的结果数为，那么从10件产品中任取3件，其中恰有k件一等品的概率为P(X=k)=,k=0,1,2,3.310CCCkk373CCCkk310373所以随机变量X的分布列是X0123P24740214071201•X的数学期望EX=1091201340724021124703310如果随机变量X服从参数为N,M,n的超几何分布，则EX=猜想：如果随机变量X服从参数为N,M,n的超几何分布，则EX=基础训练：设N=100个产品中有M=10个次品，任取n=20个，则取到的次品的均值是EX=10202100MnN47•某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量X表示选出的志愿者中女生的人数,则数学期望•EX=（结果用最简分数表示）课堂小结课堂小结一、离散型随机变量取值的平均值数学期望数学期望nniipxpxpxpxEX2211P1xix2x······1p2pip······nxnpX二、如果随机变量X服从两点分布，X10Pp1－p则pEX三、如果随机变量X服从二项分布，即X～B（n,p），则npEX四，如果随机变量X服从参数为N,M,n的超几何分布，则MEXnN作业•1．在10件产品中,有3件一等品,4件二等品,3件三等品.从这10件产品中任取3件,•求：取出的3件产品中一等品件数X的分布列和数学期望2.抛掷一枚质地均匀的硬币3次，记正面朝上的次数为X.（1）求随机变量X的分布列；（2）求随机变量X的均值