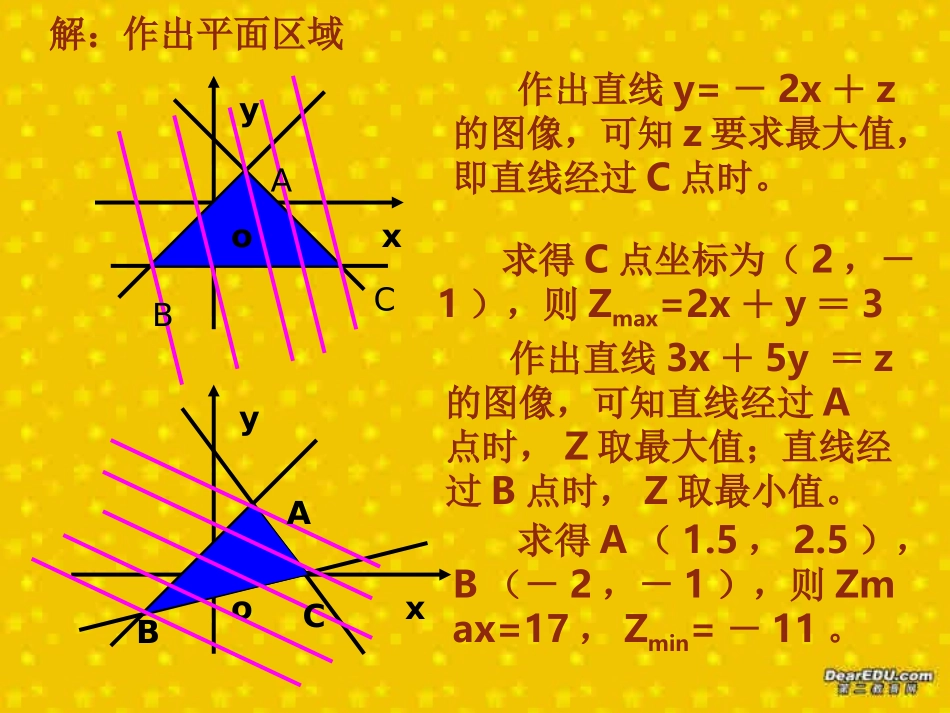
简单的线性规划问题简单的线性规划问题简单的线性规划问题简单的线性规划问题求z=2x+y的最大值,使x、y满足约束条件:11-+yyxxy求z=3x+5y的最大值,使x、y满足约束条件:35x11535yxyyx-++(一)求目标函数的最值解:作出平面区域xyABCxyooABC作出直线y=-2x+z的图像,可知z要求最大值,即直线经过C点时。求得C点坐标为(2,-1),则Zmax=2x+y=3作出直线3x+5y=z的图像,可知直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。的最大值和最小值。求满足下列条件式中变量设zxyxyxyxyxz,1255334,,2求z的最大值和最小值.设z=2x+y,式中变量x,y满足下列条件.4yx2,6yx4①•求z=2x+y的最大值,使式中的x、y满足约束条件y≤xx+y≤1y≥-1(二)应用题例1、某公司承担了每天至少搬运280t水泥任务,已知该公司有6辆A型卡车和4辆B型卡车,又知A型卡车每天每辆的运输量为30t,成本费为0.9千元;B型卡车每天每辆的运输量为40t,成本费为1千元假如你是公司的经理,为了使公司支出的费用最少,请你设计出公司每天的派出A型卡车、B型卡车各多少辆?分析:.40602843,9.0的最小值求变量满足下列条件,式中设zyxyxyxyxz问题:246810246810xoyABC0.9x+y=0.40602843,9.0的最小值求变量满足下列条件,式中设zyxyxyxyxz解:上述不等式组表示的平面区域如图所示,作一组平行直线0.9x+y=t,直线经过点A(4,4)时,对应的t的值最小,经过点B(6,4)时,对应的t的值最大,所以z的最小值为0.9×4+4=7.6答:公司派出4辆A型卡车、4辆B型卡车时每天所支出的费用最少例2、营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?食物/kg碳水化合物/kg蛋白质/kg脂肪/kgA0.1050.070.14B0.1050.140.07分析:将已知数据列成表格解:设每天食用xkg食物A,ykg食物B,总成本为z,那么00671461475770006.007.014.006.014.007.0075.010.0105.0yxyxyxyxyxyxyxyx++目标函数为:z=28x+21y作出二元一次不等式组所表示的平面区域,即可行域把目标函数z=28x+21y变形为xyo5/75/76/73/73/76/72834zxy它表示斜率为随z变化的一组平行直线系34是直线在y轴上的截距,当截距最小时,z的值最小。28zM如图可见,当直线z=28x+21y经过可行域上的点M时,截距最小,即z最小。M点是两条直线的交点,解方程组6714577yxyx得M点的坐标为:7471yx所以zmin=28x+21y=16由此可知,每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元。例3、某人准备投资1200万元兴办一所完全中学。对教育市场进行调查后,他得到了下面的数据表格(以班级为单位)分别用数学关系式和图形表示上述限制条件。若根据有关部门的规定,初中每人每年可收学费1600元,高中每人每年可收学费2700元。那么开设初中班和高中班多少个?每年收费的学费总额最多?学段班级学生数配备教师数初中45226/班2/人高中40354/班2/人万元硬件建设万元教师年薪把上面四个不等式合在一起,得到0y0x042yx30yx20++yx2030402030o另外,开设的班级不能为负,则x≥0,y≥0。而由于资金限制,26x+54y+2×2x+2×3y≤1200解:设开设初中班x个,高中班y个。因办学规模以20~30个班为宜,所以,20≤x+y≤30yx2030402030o由图可以看出,当直线Z=7.2x+10.8y经过可行域上的点M时,截距最大,即Z最大。设收取的学费总额为Z万元,则目标函数Z=0.16×45x+0.27×40y=7.2x+10.8y。Z=7.2x+10.8y变形为它表示斜率为的直线系,Z...