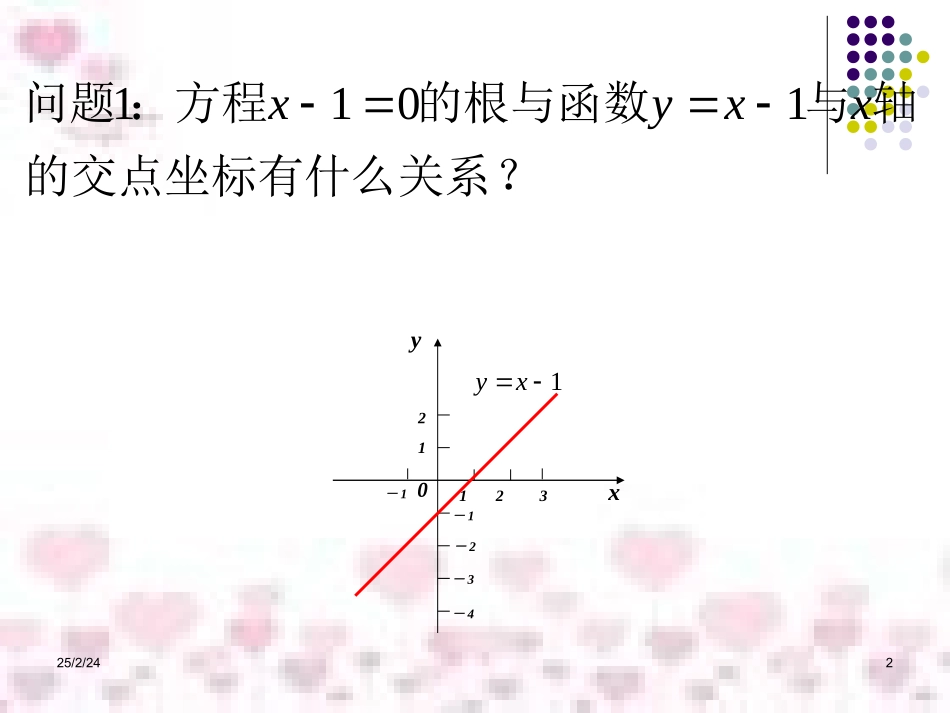
25/2/24125/2/242?的交点坐标有什么关系轴与的根与函数:方程问题xxyx1011xy0-132112-1-2-3-41xy25/2/243交点坐标。请写出轴是否有交点。若有,函数图像与像的草图。并判断画出相应的二次函数图方程的根,并:求出表中的一元二次问题x225/2/244函数的图像与x轴交点方程函数函数的图像方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点xy0-132112-1-2-3-4..........xy0-132112543.....yx0-12112x2-2x+1=0x2-2x+3=0y=x2-2x-3y=x2-2x+1x2-2x-3=0y=x2-2x+3系?思考:二者之间有何联25/2/245会有什么结论?与相应的二次函数程的一元二次方:上述结论推广至一般问题cbxaxyacbxax22)0(0325/2/246判别式=b2-4ac>00<0二次函数y=ax2+bx+c的图像一元二次方程ax2+bx+c=0的根二次函数y=ax2+bx+c的图像与x轴的交点有两个不等的实数根x1,x2有两个相等实数根x1=x2没有实数根xyx1x2xyx1=x2xy一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图像有如下关系:(x1,0),(x2,0)(x1,0)没有交点25/2/247又会有什么结论?与相应的函数般方程:将上述结论推广至一问题)(0)(4xfyxf方程的实数根就是对应函数图像与x轴交点的横坐标。结论25/2/2481、函数零点的定义对于函数,我们把使的实数x叫做函数的零点。)(xfy0)(xf)(xfy方程f(x)=0有实数根函数y=f(x)的图像与x轴有交点函数y=f(x)有零点2、结论25/2/249有几个零点?像,说一说的图函数图像寻找零点呢?观察的零点,如何根据:方程的实数根即函数问题)()(5xfyRxxfyxy025/2/2410abab问题6:如果将定义域改为区间[a,b]观察图像说一说零点个数的情况,有什么发现?abxy00)()(bfaf结论25/2/2411是否一定有零点?端点函数值上函数:如果闭区间问题0)()()(],[7bfafxfybaababxy0函数的图像在闭区间[a,b]上连续不断。)(xfy结论25/2/2412问题8:满足上述两个条件,能否确定零点个数呢?ab0yxabxy0有零点,至少有一个,但不确定个数,即存在零点。结论25/2/2413结论不断的一条曲线,上的图像是连续在区间如果函数],[)(baxfy内有零点,间在区那么,函数并且有),()(,0)()(baxfybfaf的根。也就是方程这个使得即存在0)(,0)(),,(xfccfbac25/2/2414的零点个数。:求函数问题62ln)(9xxxfx0-2-4-6105y241086121487643219表3--1x123456789f(x)-4-1.30691.09863.38635.60947.79189.945912.079414.1972解:用计算器或计算机作出的对应值表(表3--1)和图像。)(xfx、25/2/2415问题10:为什么上个问题中只有一个零点呢?说一说理由?。)是增函数,请证明它,在(函数0)(xf25/2/2416问题11:请同学们思考、交流一下,这节课学习到了什么?1、知识小结:一个定义,四个结论。2、思想方法:数形结合、转化思想。25/2/2417作业:1、必做题:P88练习第二题2、选做题:(1)在区间(0,3)范围内恰有一个零点,则a的取值范围是多少?32)(2xaxxf的实数解的个数的方程,讨论关于已知axxxRa86)2(225/2/2418一、教材、学情分析二、教学目标、重难点分析三、教法、学法分析四、教学流程25/2/2419一、教材结构与内容简析函数与方程思想是中学数学的重要思想。本节是在学习了前两章函数性质的基础上,利用函数的图象和性质来判断方程的根的存在性及根的个数,从而了解函数的零点与方程的根的关系以及掌握函数在某个区间上存在零点的判定方法;为下节“二分法求方程的近似解”和后续学习的算法提供基础.因此本节内容具有承前启后的作用,非常重要.25/2/2420二、学情分析在此之前,学生对一元二次函数和一元二次方程已经比较熟悉,会判断具体的一元二次方程有没有根,有几个根,会用求根公式求根。但是对一元二次函数与方程的联系认识不全面,也没有上升到一般的函数与方程的层次。因此,在讲解本节内容时,让学生对函数与方程的关系及零点存在定理有较为全面的认识。25/2/2421二、教学目标(一)认知目标:1.理解函数的零点与方程的根的联系.2.理解并会用零点存在定理判断函数的零点.(二)能力目标:体会数形结...