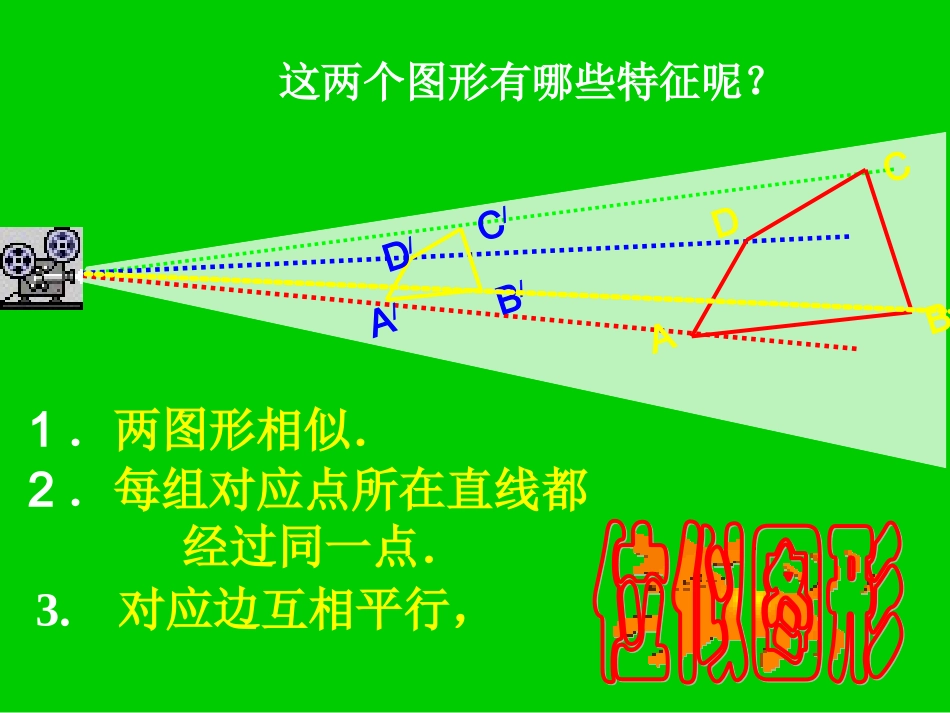
这两个图形有哪些特征呢?1.两图形相似.2.每组对应点所在直线都经过同一点.3.对应边互相平行,A/B/D/C/ABDC如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个交点叫做位似中心,这时两个相似图形的相似比又叫做它们的位似比.ABDCA/B/D/C/O1.两图形相似.同时满足下面三个条件的两个图形才叫做位似图形.三条件缺一不可.显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.2.每组对应点所在直线都经过同一点.3.对应边互相平行,如图,已知△ABCDEF∽△,它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形?0BECFAD练一练:判断下列各对图形哪些是位似图形,哪些不是.(1)正方形ABCD与正方形A′B′C′D′.(2)等边三角形ABC与等边三角形A′B′C′O练一练:判断下列各对图形哪些是位似图形,哪些不是.(3)扇形ABC与扇形A′B′C′,(B、A、B′在一条直线上,C、A、C′在一条直线上)(4)△ABC与△ADE(①DE∥BC;②∠AED=∠B)(5)五边形ABCDE与五边形A′B′C′D′E′;(1)-1(1)-2(6)在平行四边形ABCD中,△ABO与△CDO4.位似图形不一定相似。3.相似图形一定位似。2.不是位似图形必定不相似。1.位似图形必是全等图形。以下说法对吗?如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半.练习:任作一个四边形ABCD。作出它的位似图形,使它放大1倍。2.位似图形上任意一对对应点到位似中心的距离之比等于位似比.CBB/C/OA/AABDCEFP1.位似图形的对应点和位似中心在同一条直线上位似图形有以下性质:如图,D,E分别AB,AC上的点.(1)如果DEBC∥,那么∆ADE和∆ABC是位似图形吗?为什么?ABCDE解:(1)∆ADE和∆ABC是位似图形.理由是:DEBC∥,所以∠ADE和=∠B,∠AED=∠C.所以∆ADE∆ABC.∽又因为点A是∆ADE和∆ABC的公共点,点D和点B是对应点,点E和点C是对应点,直线BD与CE交于点A,所以∆ADE和∆ABC是位似图形.如图,D,E分别AB,AC上的点.(1)如果DEBC∥,那么∆ADE和∆ABC是位似图形吗?为什么?ABCDE(2)如果∆ADE和∆ABC是位似图形,那么DEBC∥吗?为什么?解:(2)DEBC.∥理由是:∆ADE和∆ABC是位似图形,∆ADE∆ABC∽∠ADE=∠BDEBC.∥培养逆向思维在下图中,(1),(3)中的两个图形是位似图形,(2)中的两个图形不是位似图形.分别指出图(1),(3)各自的位似中心;OP(1)(3)(2)灵感智慧课堂小结1.位似图形的概念2.位似图形的性质位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.(位似比)如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个交点叫做位似中心,这时两个相似图形的相似比又叫做它们的位似比.