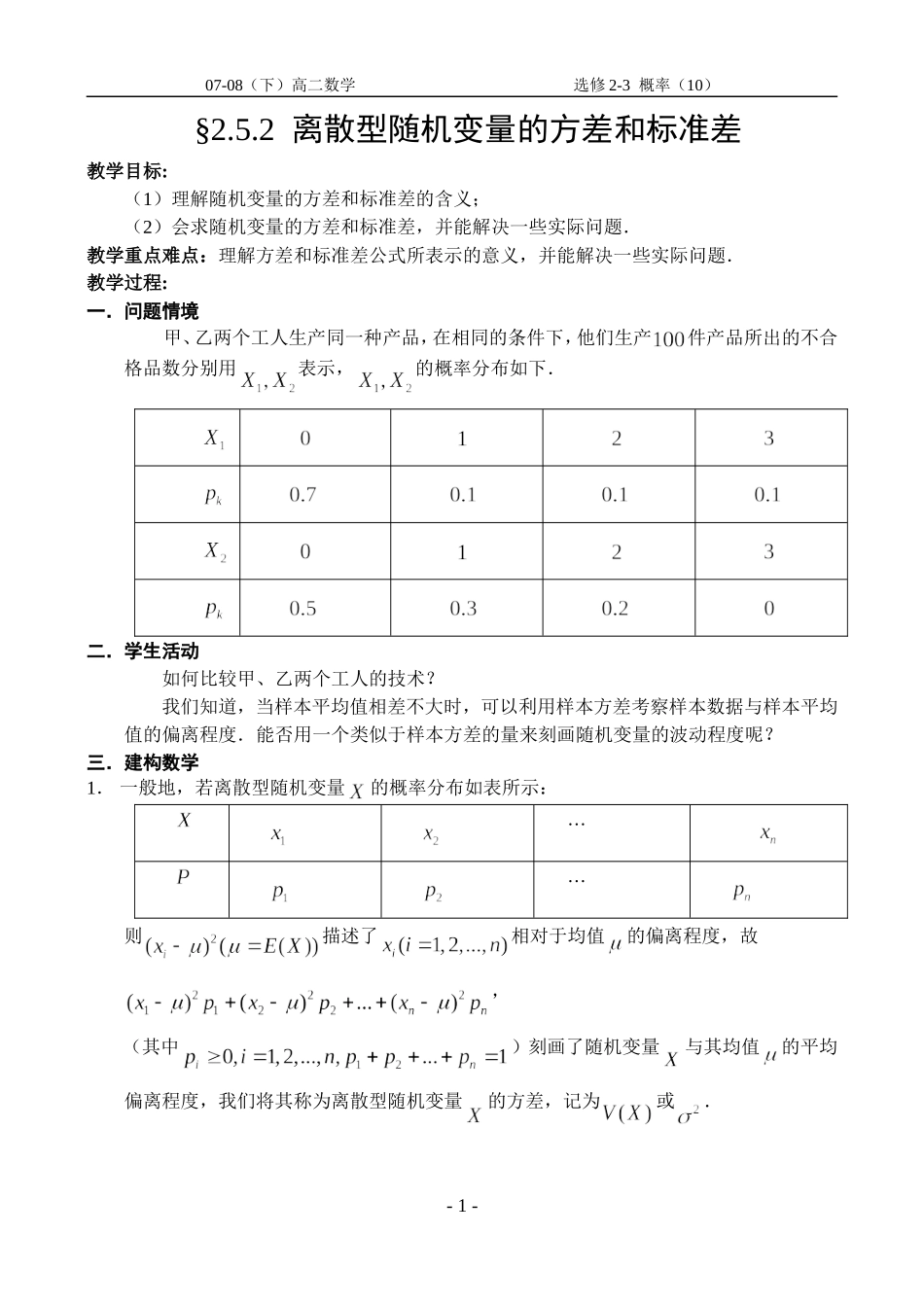
07-08(下)高二数学选修2-3概率(10)§2.5.2离散型随机变量的方差和标准差教学目标:(1)理解随机变量的方差和标准差的含义;(2)会求随机变量的方差和标准差,并能解决一些实际问题.教学重点难点:理解方差和标准差公式所表示的意义,并能解决一些实际问题.教学过程:一.问题情境甲、乙两个工人生产同一种产品,在相同的条件下,他们生产件产品所出的不合格品数分别用表示,的概率分布如下.二.学生活动如何比较甲、乙两个工人的技术?我们知道,当样本平均值相差不大时,可以利用样本方差考察样本数据与样本平均值的偏离程度.能否用一个类似于样本方差的量来刻画随机变量的波动程度呢?三.建构数学1.一般地,若离散型随机变量的概率分布如表所示:……则描述了相对于均值的偏离程度,故,(其中)刻画了随机变量与其均值的平均偏离程度,我们将其称为离散型随机变量的方差,记为或.-1-07-08(下)高二数学选修2-3概率(10)2.方差公式也可用公式计算.3.随机变量的方差也称为的概率分布的方差,的方差的算术平方根称为的标准差,即.4.随机变量的方差和标准差都反映了随即变量的取值偏离于均值的平均程度。方差或标准差越小,随即变量偏离于均值的平均程度就越小。5.对于上述问题,通过计算可得,,这说明乙的技术稳定性较好。四.数学运用例1.若随机变量的分布如表所示:求方差和标准差.01例2.求第节例1中超几何分布的方差和标准差.-2-07-08(下)高二数学选修2-3概率(10)例3.求第节例2中的二项分布的方差和标准差.说明:一般地,由定义可求出超几何分布和二项分布的方差的计算公式:当时,,当时,.例4.有甲、乙两名学生,经统计,他们在解答同一份数学试卷时,各自的成绩在80分、90分、100分的概率分布大致如下表所示。试分析两名学生的答题成绩水平。-3-甲分数8090100概率乙分数8090100概率07-08(下)高二数学选修2-3概率(10)五.回顾小结:1.离散型随机变量的方差和标准差的概念和意义;2.离散型随机变量的方差和标准差的计算方法;3.超几何分布和二项分布的方差和标准差的计算方法.六.课外作业:课本P712,3,4,5,6-4-